Bacterial Growth Curve - Definition, Phases, Calculations, Factors, Importance

What is Bacterial Growth Curve?

The bacterial growth curve is a graphical representation that illustrates the different phases of bacterial growth over time. It provides valuable insights into the growth patterns and dynamics of bacterial populations.

The curve typically consists of four distinct phases: lag phase, log phase (exponential growth phase), stationary phase, and death phase. These phases reflect the changes in the number, size, and mass of bacterial cells during their growth cycle.
Several factors influence bacterial growth, including temperature, pH, oxygen availability, nutrient availability, and moisture content. Bacteria are prokaryotic and unicellular organisms that primarily reproduce through a process called binary fission, where one parent cell divides into two identical daughter cells.
To study the bacterial growth curve, certain measures need to be considered. First, a suitable culture medium must be provided to support the growth of microorganisms. As the bacteria utilize the nutrients in the culture medium, cell division occurs in a logarithmic or exponential pattern.

Therefore, the growth of bacteria is typically expressed in logarithmic units rather than arithmetic units. This exponential growth results in a non-linear graph, with the number of bacteria increasing rapidly over time.
Distinct growth phases can be observed by incubating the bacteria at different time intervals. The lag phase is an initial period of adjustment during which the bacteria adapt to their new environment.
In the log phase, bacterial growth is at its maximum, with the number of viable bacteria increasing exponentially. This phase is of particular interest in microbiological research and various applications. The stationary phase occurs when the rate of cell division equals the rate of cell death, resulting in a stable population size. Finally, the death phase is characterized by a decline in the number of viable bacteria, often due to nutrient depletion and accumulation of waste products.

Measuring the growth rate of bacteria and studying the growth curve is crucial in microbiology. It is a fundamental technique used in basic research, as well as in agricultural and industrial applications.
Understanding the growth patterns of bacteria helps researchers and industries optimize conditions for bacterial growth, such as in fermentation processes, food production, and the development of antimicrobial agents. By monitoring the growth curve, scientists can gain insights into the growth kinetics, survival strategies, and behavior of bacteria in various environments.

Definition of Bacterial Growth Curve

The bacterial growth curve is a graphical representation of the different phases of bacterial growth over time, including the lag phase, log phase, stationary phase, and death phase.

Binary Fission of Bacteria – Understand the Bacterial Growth

(a) The electron micrograph depicts two cells of Salmonella typhimurium after a binary fission event. (b) Binary fission in bacteria starts with the replication of DNA as the cell elongates. A division septum forms in the center of the cell. Two daughter cells of similar size form and separate, each receiving a copy of the original chromosome. (credit a: modification of work by Centers for Disease Control and Prevention) | Image Source: https://courses.lumenlearning.com

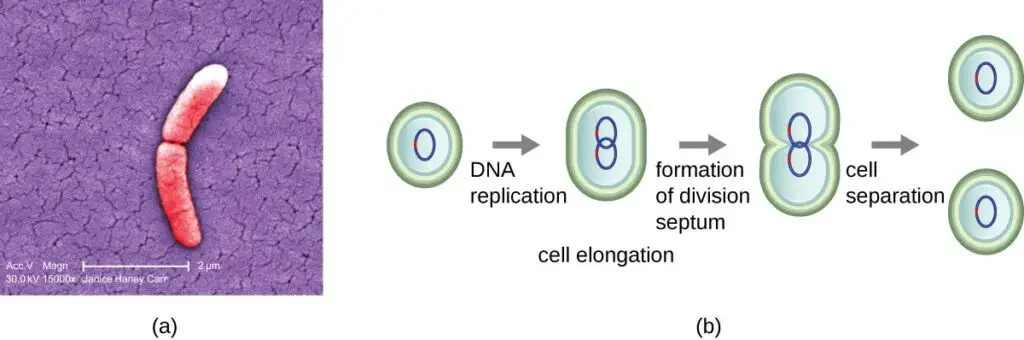
Binary fission is the most common mechanism of cell replication in bacteria. It involves a series of steps that lead to the division of a single bacterial cell into two daughter cells.
The process of binary fission begins with the cell undergoing growth and an increase in the number of cellular components. During this growth phase, the replication of DNA starts at a specific location on the circular chromosome known as the origin of replication. The circular chromosome is attached to the inner cell membrane. DNA replication proceeds in opposite directions along the chromosome until it reaches a region called the terminus.
As the cell continues to grow, the center of the enlarged cell starts to constrict. This constriction eventually leads to the formation of two daughter cells. Each daughter cell receives a complete copy of the parental genome, ensuring that the genetic material is passed on accurately. Additionally, the cytoplasm is divided between the two daughter cells in a process known as cytokinesis.

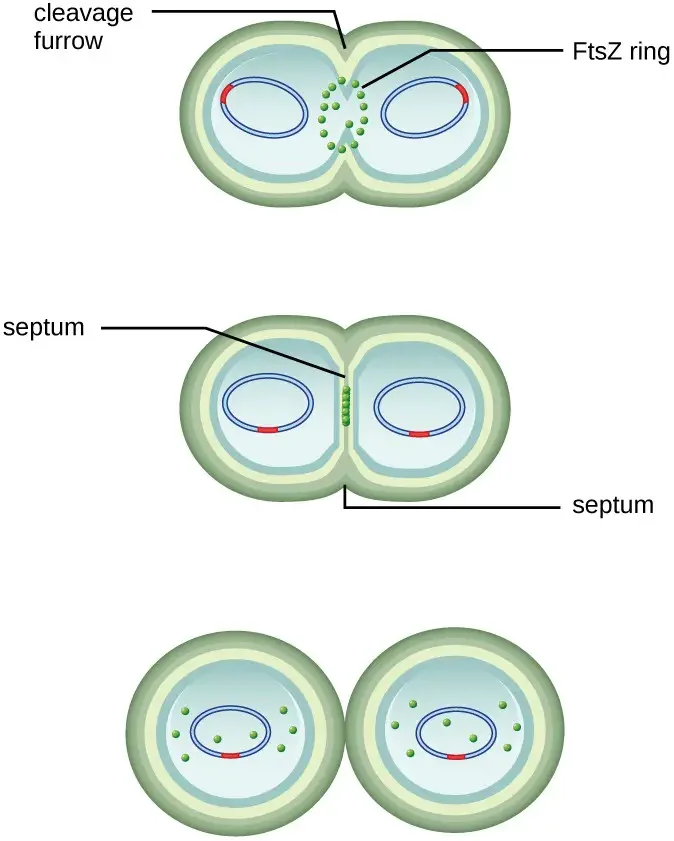
The protein FtsZ plays a crucial role in directing cytokinesis and cell division. FtsZ assembles into a structure called the Z ring on the cytoplasmic membrane. This Z ring is anchored by FtsZ-binding proteins and serves as a marker for the division plane between the two daughter cells. Other proteins essential for cell division are recruited to the Z ring, forming a complex known as the divisome.
Once the divisome is fully assembled, it activates the production of a peptidoglycan cell wall and initiates the formation of a septum that divides the two daughter cells. The peptidoglycan cell wall is a key component of bacterial cell structure and provides strength and rigidity. Specific enzymes are involved in breaking the bonds between the monomers in the existing peptidoglycan layer, allowing the addition of new subunits along the division septum.
During division, all of the outer layers of the cell, including the cell wall and outer membranes if present, must be remodeled to complete the process. This remodeling involves the coordinated action of various enzymes and proteins.

Overall, binary fission is a highly orchestrated process in which a single bacterial cell replicates its genetic material, divides the cytoplasm, and forms two daughter cells. It relies on the precise assembly and activation of proteins such as FtsZ and the divisome, as well as the remodeling of the cell wall and outer layers to ensure successful cell division.

FtsZ proteins assemble to form a Z ring that is anchored to the plasma membrane. The Z ring pinches the cell envelope to separate the cytoplasm of the new cells. | Image Source: https://courses.lumenlearning.com

Requirements for Bacterial Growth

Chemical or Nutrient Requirement

Chemical or nutrient requirements are essential for bacterial growth and metabolism. Different bacterial species have varying requirements for carbon, nitrogen, sulfur, phosphorus, trace elements, and oxygen. Additionally, the culture medium used in laboratory conditions plays a crucial role in providing the necessary nutrients for bacterial growth.

Carbon Source: Carbon is a major component of bacterial cells, making up about 50% of their dry weight. Bacterial species have different carbon requirements:

Chemoheterotrophs obtain carbon from organic sources such as proteins, lipids, and carbohydrates. They may also utilize complex compounds like vitamins and growth factors.
Chemoautotrophs and photoautotrophs primarily obtain carbon from carbon dioxide (CO2).

Nitrogen Source: Nitrogen is an essential element required for building amino acids, RNA, and DNA. While most bacterial species use proteins as their nitrogen source, nitrogen-fixing bacteria have the ability to directly obtain nitrogen from the atmosphere. Some bacteria rely on nitrate salts as their nitrogen source.

Sulfur Source: Sulfur is necessary for the formation of certain proteins and vitamins like biotin and thiamine. Bacterial species obtain sulfur from proteins, hydrogen sulfide, and sulfates.

Phosphorus Source: Phosphorus is crucial for building DNA, RNA, ATP, and phospholipids. Bacterial species obtain phosphorus from inorganic phosphate salts and buffers.

Trace Elements: Trace elements serve as cofactors for enzymes and include elements like iron, copper, zinc, and molybdenum. These elements are essential for proper enzyme function and bacterial metabolism.

Oxygen: Bacteria have varying oxygen requirements, which categorize them into different groups:

Obligate aerobes require oxygen for their survival, such as Pseudomonas.
Obligate anaerobes cannot tolerate oxygen and live in environments devoid of oxygen, for example, Clostridium.

Facultative anaerobes can live with or without oxygen and adapt their metabolism accordingly. Examples include Staphylococcus and Escherichia coli.
Aerotolerant anaerobes do not require oxygen for growth but can tolerate its presence. They can also break down toxic forms of oxygen. An example is Lactobacillus caries.
Microaerophiles require a low concentration of oxygen to grow but are sensitive to high levels of oxygen and its toxic forms like hydroxyl radicals.

Culture Medium: In laboratory conditions, a culture medium is used to provide the necessary nutrients and minerals for bacterial growth. The composition of the medium is tailored to meet the specific requirements of the bacterial species being cultured. Culture media can be prepared in different forms, including solid, semi-solid, or liquid, by varying agar concentrations. These media provide the necessary carbon, nitrogen, sulfur, phosphorus, trace elements, and other essential components required for bacterial growth and metabolism.

By understanding the specific chemical and nutrient requirements of bacterial species, researchers can optimize culture conditions and provide suitable environments for their growth and study.

Physical Requirements

Physical requirements play a crucial role in bacterial growth and survival. Factors such as pH, temperature, and osmotic pressure significantly impact bacterial growth and metabolism.

pH: Bacterial species exhibit preferences for different pH levels, and they can be categorized into three groups based on their pH requirements:

Acidophiles are acid-loving bacteria that thrive in environments with a pH range of 0.1 to 5.4.
Neutrophiles prefer a pH range of 5.4 to 8.5, which is closer to neutral conditions.

Alkaliphiles are bacteria that prefer alkaline conditions, with a pH range of 7 to 12 or even higher.

Temperature: Bacterial species have different temperature preferences, and they can be classified into three groups based on their temperature requirements:

Mesophiles are bacteria that thrive at moderate temperatures, typically between 25°C to 40°C. Many common bacterial pathogens, including Escherichia coli and Staphylococcus aureus, are mesophiles.

Psychrophiles are cold-loving bacteria that can survive and grow at temperatures between 0°C to 20°C. They are commonly found in cold environments such as polar regions.
Thermophiles are heat-loving bacteria that thrive in high-temperature environments, typically ranging from 50°C to 60°C. These bacteria can be found in hot springs and geothermal areas.

Osmotic Pressure: Bacterial cells contain a high percentage of water, usually around 80-90%. Changes in osmotic pressure can have a significant impact on bacterial cells:

Hypertonic solutions with increased solute concentration can cause water to move out of bacterial cells, leading to plasmolysis, where the cell membrane shrinks away from the cell wall. This can inhibit bacterial growth and metabolism.
Hypotonic solutions with lower solute concentration than the bacterial cytoplasm can cause water to enter the cells rapidly, potentially leading to cell lysis or bursting.

Maintaining appropriate osmotic pressure is essential for bacterial cells to function properly. Some bacteria have adapted mechanisms to tolerate and survive in environments with high or low osmotic pressure, such as the production of osmoprotectants or the regulation of ion transport.

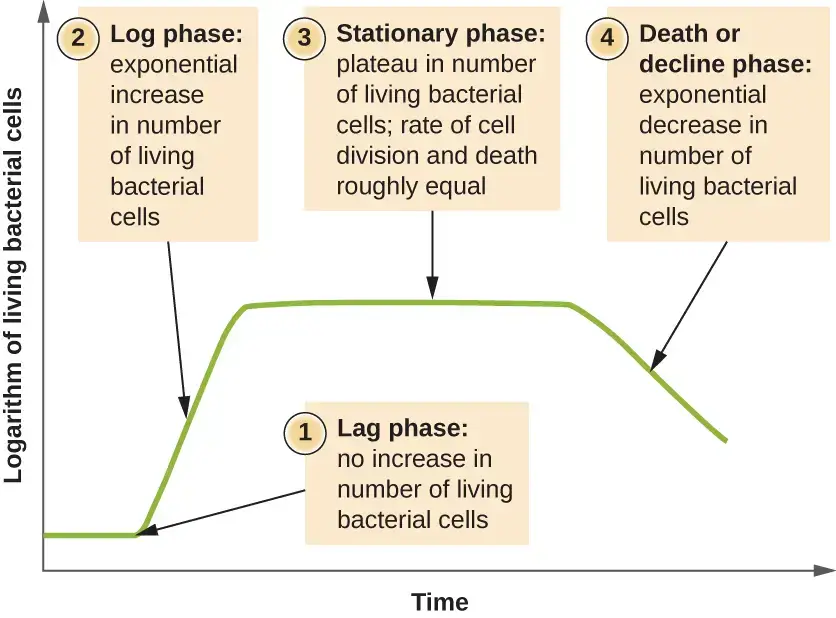
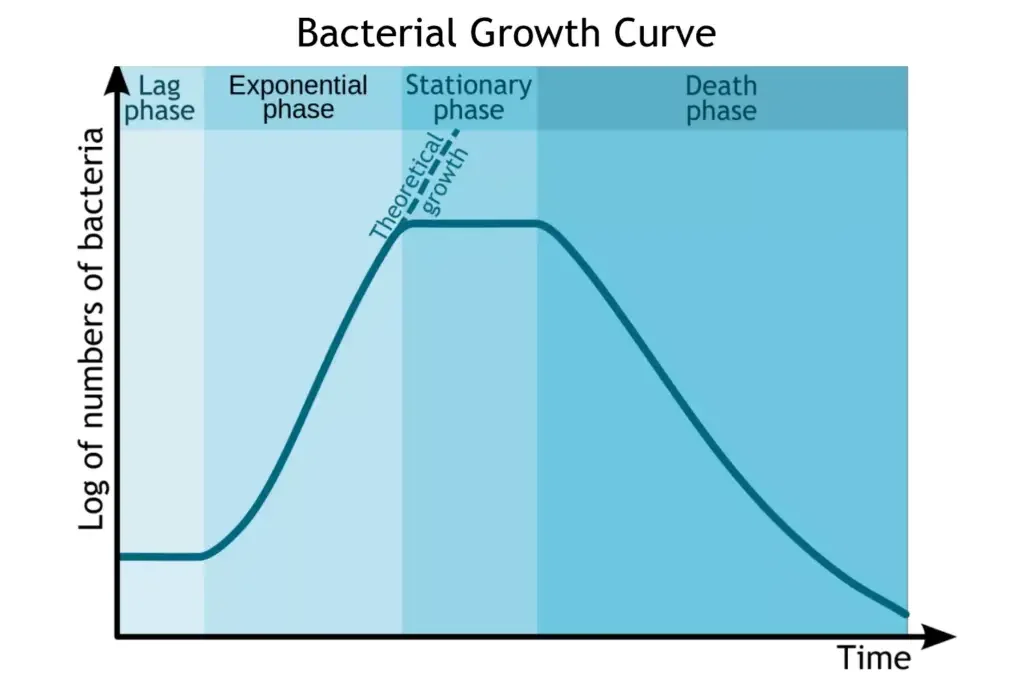
Phases of Bacterial Growth Curve

The growth curve has following phases

Lag phase
Log phase or exponential phase

Stationary phase
Death phase or decline phase

1. Lag phase of Bacterial Growth Curve

The lag phase of the bacterial growth curve is the initial phase after inoculation into a fresh medium where the population of bacteria remains temporarily unchanged.

During this phase, there is no apparent cell division occurring, but the cells undergo various metabolic activities and preparations for growth. These activities include increasing in volume or mass, synthesizing enzymes, proteins, RNA, and other molecules, and adapting to the new growth conditions.
The length of the lag phase depends on several factors, such as the size of the inoculum, time needed for recovery from physical damage or shock during transfer, synthesis of essential coenzymes or division factors, and synthesis of new enzymes necessary for metabolizing the substrates present in the medium.
The lag phase is a period of adjustment for the bacteria to the new environment. While there is little to no cell division during this phase, the cells are not dormant.

Instead, they are actively preparing for subsequent growth. The length of the lag phase can vary from 1 hour to several days, depending on the specific conditions and the bacterial species involved.
At the end of the lag phase, the bacteria become fully prepared for cell division and enter the exponential growth phase of the growth curve.

Lag phase Key Points

The lag phase is the initial phase of the bacterial growth curve after inoculation into a fresh medium.

During the lag phase, there is no apparent increase in the number of bacterial cells, but the cells undergo metabolic activities and preparations for growth.
Bacteria in the lag phase are metabolically active and undergo processes such as synthesis of enzymes, proteins, RNA, and other molecules.
The length of the lag phase varies depending on factors such as the size of the inoculum, time required for recovery from physical damage or shock, and synthesis of essential coenzymes or division factors.

Bacteria in the lag phase are adapting to the new growth conditions and adjusting to the environment, including temperature and atmospheric conditions.
The lag phase is a period of adjustment necessary for the synthesis of enzymes and coenzymes for physiological activities.
The duration of the lag phase can vary depending on the bacterial species, the nature of the culture medium, and the incubation temperature.

If the bacteria are transferred from a rich medium to a nutritionally poor medium, the lag phase is longer due to the time required for adaptation.
Conversely, if the bacteria are transferred from a nutritionally poor medium to a rich medium, the lag phase may be shorter or absent as they can readily adapt to the favorable conditions.
At the end of the lag phase, the bacteria become fully prepared for cell division and enter the log phase, where exponential growth occurs.

2. Log phase or exponential phase

The exponential phase is characterized by balanced growth, where all the cells are dividing regularly through binary fission and growing by geometric progression. The rate of cell division and growth is constant during this phase, depending on the composition of the growth medium and incubation conditions. The growth rate is expressed as the generation time, which is the time required for the population to double.
During the log phase, the number of new bacteria appearing per unit of time is proportional to the present population. If growth conditions are optimal and not limited, the number of cells and the rate of population increase double with each consecutive time period. When the natural logarithm of cell number is plotted against time, it results in a straight line, and the slope of this line represents the specific growth rate of the organism. The specific growth rate is a measure of the number of divisions per cell per unit time.
In the log phase, bacteria divide continuously at a constant rate, resulting in exponential growth. The bacteria are in their rapid stage of cell division and exhibit balanced growth. They have the smallest size during this phase. The metabolic activities, chemical composition of cells, and physiological characteristics of the bacteria are nearly uniform in the population during the log phase. This phase is often used to identify bacteria based on their biochemical and physiological characteristics.

The generation time of bacteria is usually determined during the log phase, although it can vary among different bacterial species and growth conditions. It is the shortest during the log phase and is influenced by the growth factors present in the medium. The log phase can last for several hours, depending on the organism type, growth conditions, and population density.
The exponential or log phase is a period of intense metabolic activity for microorganisms, during which primary metabolites are produced, enhancing the growth rate in terms of increased cell number and size. Microorganisms in this phase exhibit resistance to adverse conditions such as antibiotics and radiation. The number of cells produced exceeds the number of cells dying during the exponential phase.
Overall, the exponential phase is crucial for the rapid growth and multiplication of bacteria, characterized by balanced growth, high metabolic activity, and increased biomass production.

Log phase Key Points

The log phase, also known as the exponential phase, is the second phase of the bacterial growth curve.
During the log phase, bacteria are actively dividing and replicating their DNA.
The number of bacteria in the population increases exponentially during this phase, doubling at a constant rate.

The rate of bacterial growth in the log phase is determined by factors such as the availability of nutrients, temperature, pH, and other environmental conditions.
The log phase is characterized by balanced growth, where all cells are dividing regularly through binary fission.
Bacterial growth during the log phase follows a geometric progression, with the number of cells and the rate of population increase doubling with each consecutive time period.

The growth rate during the log phase is expressed as the generation time, which is the time required for the population to double.
Bacteria in the log phase are at their most metabolically active and produce large amounts of biomass.
The log phase is often used to determine the specific growth rate of bacteria, which is a measure of the number of divisions per cell per unit time.

The metabolic activities, chemical composition, and physiological characteristics of bacteria are relatively uniform in the log phase.
The log phase is a period of rapid growth and is crucial for the multiplication and expansion of bacterial populations.
The duration of the log phase can vary depending on the type of organism, growth conditions, and population density.

3. Stationary Phase

The stationary phase is the third phase of the bacterial growth curve, following the log phase:

The stationary phase occurs when bacterial growth slows down and eventually stops due to various factors such as nutrient depletion, accumulation of waste products, changes in pH, and limited oxygen availability.
During the stationary phase, the rate of cell division is equal to the rate of cell death, resulting in a state of equilibrium. The number of new cells created is limited by growth factors, leading to a stable population size.

Bacteria in the stationary phase undergo changes in their physiology and metabolism to adapt to the challenging environment. They enter a state of dormancy or quiescence to conserve energy and resources.
Some bacteria in the stationary phase may produce secondary metabolites such as antibiotics. This is a survival strategy that can help inhibit the growth of competing organisms and enhance their own chances of survival.
Bacterial cells in the stationary phase may also undergo sporulation, a process in which they form highly resistant spores that can survive harsh conditions and enable future growth when conditions become favorable again.

The stationary phase is characterized by a decrease in metabolic activity and a slowdown in the synthesis of cell components. Bacterial cells become less susceptible to antibiotics and may show irregular staining patterns.
Mutations can occur during the stationary phase, as DNA damage caused by endogenously generated reactive oxygen species becomes a major source of genetic changes.
The stationary phase represents a critical stage in the bacterial growth cycle and is an important area of study for understanding bacterial survival strategies, antibiotic resistance, and other biological processes.

If cells from the stationary phase are transferred to a fresh nutrient-rich medium, they can transition back to the log phase and resume their normal metabolic activities.

Overall, the stationary phase is a period of adaptation and survival for bacteria when growth conditions become unfavorable, allowing them to persist until more favorable conditions arise.

Stationary Phase Key Points

Here are some key points about the stationary phase in bacterial growth:

The stationary phase is the third phase of the bacterial growth curve, following the lag phase and the log/exponential phase.
During the stationary phase, the growth rate of the bacterial population becomes nearly zero. The number of new cells being produced is balanced by the number of cells dying, resulting in a relatively stable population size.
The stationary phase occurs when one or more growth-limiting factors come into play. These factors can include the depletion of essential nutrients, the accumulation of toxic waste products, a decrease in oxygen availability, or changes in pH.

Bacteria in the stationary phase undergo physiological and metabolic changes to adapt to the challenging conditions. They may enter a state of dormancy or quiescence, reducing their metabolic activity to conserve energy and resources.
Bacterial cells in the stationary phase often exhibit increased resistance to adverse conditions, such as antibiotics, radiation, or environmental stressors. They may undergo changes in cell morphology and become more resistant to external challenges.
Secondary metabolite production often occurs during the stationary phase. Some bacteria produce compounds like antibiotics, enzymes, or pigments during this phase as a survival strategy or a response to environmental cues.

The stationary phase is associated with the formation of endospores in certain bacterial species. Endospores are highly resistant structures that protect the bacteria from harsh conditions and facilitate their survival until favorable conditions return.
Although bacterial growth may have stopped, various cellular processes continue during the stationary phase. These processes include the synthesis of stress response proteins, DNA repair mechanisms, and the activation of survival strategies.
The duration of the stationary phase can vary greatly depending on the bacterial species, growth conditions, and the availability of nutrients. It may last from hours to weeks, and in some cases, the stationary phase can be prolonged indefinitely.

The stationary phase is of significant importance in various fields, including microbiology, biotechnology, and medicine. Understanding the behavior and characteristics of bacteria in this phase is crucial for studying antibiotic resistance, microbial ecology, and the optimization of industrial processes.

In summary, the stationary phase represents a period of equilibrium and adaptation for bacterial populations when growth becomes limited due to unfavorable conditions. Bacteria employ various survival strategies during this phase to ensure their persistence until more favorable conditions are available.

4. Death Phase

The death phase is the fourth and final phase of the bacterial growth curve, following the stationary phase.

During the death phase, the bacterial population declines as cells die off. This decline is primarily caused by two factors: the accumulation of toxic waste products and autolytic enzymes and the exhaustion of available nutrients.
In the death phase, the number of viable bacteria decreases continuously and exponentially. The total count of bacteria may remain relatively constant, but the viable count decreases as more cells die.
The death phase is characterized by the presence of involuted forms of bacteria. These forms may exhibit various shapes, such as long filamentous rods, branching or globular forms, or cells without a cell wall known as protoplasts, spheroplasts, or L-phase variants. However, when these involuted forms are transferred to a fresh nutrient medium, they usually revert to their original healthy bacterial shape.
The death rate during this phase is slower than the growth rate observed during the log/exponential phase. Not all bacteria die at the same rate, as some may be more resistant and remain viable for a longer time. For example, spore-forming bacteria can withstand harsh conditions and persist longer than other bacterial cells.
The death phase is brought about by various factors, including the depletion of essential nutrients and the accumulation of toxic waste products. As the nutrients become scarce and waste products accumulate, the conditions become increasingly unfavorable for bacterial survival, leading to cell death.
If the incubation of the bacterial population continues after reaching the stationary phase, a death phase follows. During this phase, the viable cell population declines geometrically or exponentially, which is essentially the reverse of the exponential growth observed during the log phase.
Autolysis, the process of self-destruction, occurs during the death phase. Bacterial cells break down and release their contents into the environment, contributing to the accumulation of waste materials.
The death phase is influenced by factors such as temperature, nutrient availability, oxygen levels, and other injurious conditions. The rate and duration of the death phase can vary depending on these factors and the specific bacterial species.
In some industries, continuous cultures are maintained to sustain the logarithmic growth phase of cells by periodically supplying nutrients and maintaining the appropriate aerobic conditions. This allows the bacteria to avoid entering the death phase and prolong their growth.

Measurement of Bacterial Growth

Measuring bacterial growth is essential for studying bacterial populations and understanding their growth dynamics. Several methods are commonly used to measure bacterial growth:

1. Direct Cell Count

(This method involves directly counting the number of bacterial cells in a liquid culture. A Petroff-Hausser chamber or a specialized counting chamber, such as a hemocytometer, is used for microscopic observation and cell counting. This method provides an accurate cell count but can be time-consuming and labor-intensive.)

Direct cell count is a method used to estimate the number of cells in a liquid culture or colonies on a plate. It provides a direct and relatively fast way of determining the quantity of organisms present in a sample. There are several techniques for conducting direct cell counts.
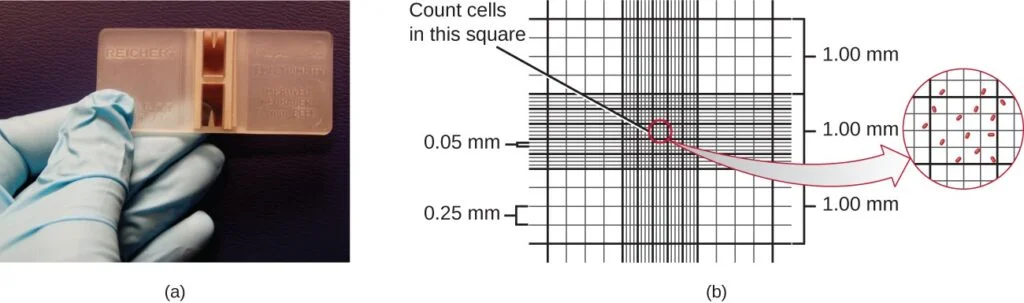
One common method is the direct microscopic cell count using a Petroff-Hausser chamber. The Petroff-Hausser chamber is a calibrated slide that contains a grid of squares of various sizes.
A known volume of the culture suspension is placed on the chamber, and a coverslip is positioned at a specific height above the grid. By counting the cells in multiple squares and calculating the observed volume, the concentration of cells in the original sample can be estimated.
If the sample was diluted before counting, the concentration must be corrected accordingly. It is important to count cells in several squares and take an average to ensure accurate measurements. This method is relatively easy, fast, and cost-effective. However, it may not be suitable for dilute cultures with low cell counts.
Fluorescence staining techniques can be employed to differentiate between viable and dead bacterial cells in a sample. Viability stains that bind to nucleic acids can be used to distinguish live cells from dead cells. The primary stain fluoresces green and can penetrate intact cytoplasmic membranes, staining both live and dead cells. The secondary stain fluoresces red and can only stain cells with significantly damaged cytoplasmic membranes. Live cells will appear green, while dead cells will appear red when observed under a fluorescence microscope. This method allows for the differentiation of viable and non-viable cells.
Another technique involves using an electronic cell counting device known as a Coulter counter. This method utilizes changes in electrical resistance to detect and count cells in a saline solution. Cells passing through a small aperture in the device cause brief changes in resistance between two electrodes, which are recorded by an electronic sensor. Each resistance change corresponds to a cell, providing a rapid and accurate count within a specific concentration range. However, if the culture is too concentrated, multiple cells passing through the aperture simultaneously can skew the results. Additionally, this method does not distinguish between live and dead cells.
Direct cell counts provide an estimation of the total number of cells in a sample. However, in many situations, it is essential to determine the number of live or viable cells. Live cell counts are crucial for assessing infections, evaluating the effectiveness of antimicrobial compounds and medications, and determining food and water contamination levels.

(a) A Petroff-Hausser chamber, (b) This diagram illustrates the grid of a Petroff-Hausser chamber, | Image Source: https://courses.lumenlearning.com

Procedure

The steps involved in a direct cell count are as follows:

Sample Preparation: Obtain a representative sample containing the cells of interest.
Petroff-Hausser Chamber: Place a known volume of the sample onto a Petroff-Hausser chamber slide.
Coverslip Placement: Position a coverslip over the chamber at a specific height from the grid.
Microscopic Examination: Use a light microscope to observe the cells in the chamber.
Cell Counting: Count the cells in multiple squares of the grid and record the numbers.
Average Calculation: Calculate the average number of cells per square based on the counts.
Volume Estimation: Determine the volume of the sample observed in the squares.
Concentration Calculation: Estimate the concentration of cells in the original sample by considering the observed volume and average cell count.
Dilution Correction (if applicable): Correct the concentration calculation if the sample was diluted before counting.
Replicate Counts: Repeat the counting process in multiple squares or multiple chambers for reliable and representative data.
Fluorescence Staining (optional): If needed, use fluorescence staining techniques to differentiate between viable and dead cells.
Electronic Cell Counting (optional): Alternatively, use an electronic cell counting device (Coulter counter) to detect and count cells based on changes in electrical resistance.
Data Analysis: Analyze and interpret the data obtained from the cell counts, considering the total cell count, live cell count, or other relevant parameters.

2. Plate Count

(The plate count method is based on the ability of viable bacteria to form colonies on nutrient agar plates. The culture is serially diluted to obtain a countable range of colonies, which are then counted after incubation under suitable conditions. The results are expressed as colony-forming units (CFUs) per milliliter of the original culture. This method provides information about viable, culturable cells and is commonly used for estimating the total number of viable cells in a sample.)

Plate count, also known as viable plate count, is a method used to estimate the number of viable or live cells in a sample. The procedure involves incubating the sample under suitable conditions and counting the resulting visible colonies. The results are typically expressed as colony-forming units per milliliter (CFU/mL) rather than cells per milliliter, as multiple cells may contribute to the formation of a single colony. The plate count is considered a low estimate of live cell numbers due to factors like viable but nonculturable cells and clustering of cells.
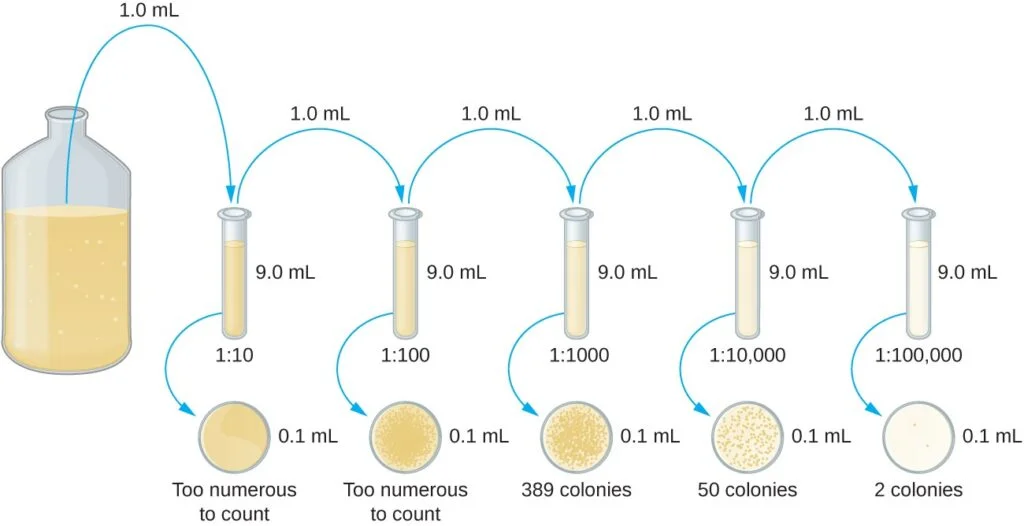
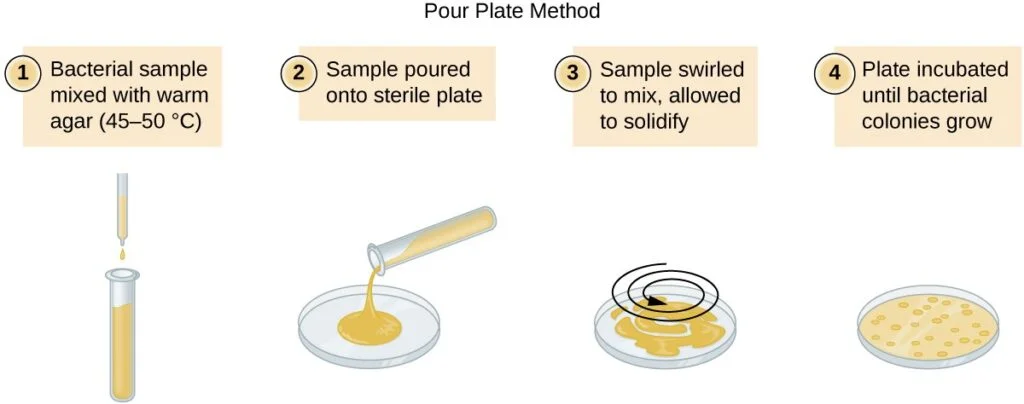
The plate count method requires two common approaches: the pour plate method and the spread plate method. Both methods begin with a serial dilution of the culture. Serial dilution involves diluting the culture in multiples of 10 to obtain plates with colony counts ranging from 30 to 300, which ensures statistically reliable results. The dilution process involves mixing a fixed volume of the original culture with dilution solution, and subsequent dilutions are made using the previous dilution as an inoculum.
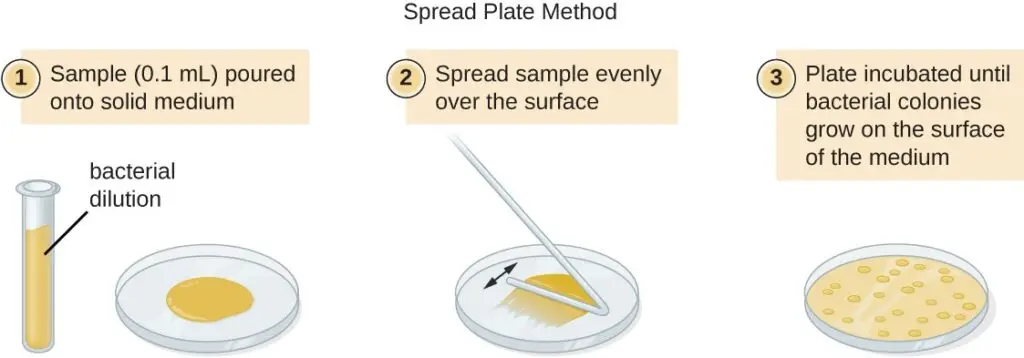
After serial dilution, samples from each dilution are plated on solid medium using either the pour plate or spread plate method. In the pour plate method, the sample is mixed with warm agar and poured into a sterile Petri dish, while in the spread plate method, the sample is poured onto solid agar and spread evenly over the surface. The plates are then incubated until colonies appear. Typically, two to three plates are prepared from each dilution, and the colony counts are averaged.
The dilution factor is used to calculate the number of cells in the original culture. The number of colonies counted on the plates, along with the dilution factor, is used to determine the colony-forming units per milliliter (CFU/mL) of the original culture.
In cases where the sample is very dilute, such as drinking water, the membrane filtration technique is used. This technique involves filtering known volumes of the sample through a membrane with a small pore size to trap microorganisms. The membrane is then transferred to a Petri plate containing growth medium, and colonies are counted after incubation. Cell density is calculated by dividing the cell count by the volume of filtered liquid.
Plate count provides an estimate of live bacterial numbers and is commonly used to assess infection extent, evaluate antimicrobial effectiveness, and detect food and water contamination. It is important to adhere to proper dilution techniques, use appropriate medium, and follow standardized protocols to ensure accurate and reliable results.

Serial dilution | Image Source: https://courses.lumenlearning.com

Procedure

The steps involved in a plate count, specifically using the pour plate or spread plate method, are as follows:

Serial Dilution: Start with a known volume of the original culture and mix it with a dilution solution. This creates the first dilution. Take a sample from this dilution and mix it with a fresh dilution solution to create the next dilution. Repeat this process, creating a series of dilutions that cover the desired cell concentration range. Each dilution represents a specific dilution factor.
Pour Plate Method: a. Take a Petri dish and pour warm agar (at around 45-50°C) into it. b. Add a sample from a specific dilution to the agar in the Petri dish. c. Swirl the Petri dish gently to ensure even distribution of the sample within the agar. d. Allow the agar to solidify. e. Incubate the Petri dish at suitable conditions for the growth of the target bacteria. f. Count the resulting colonies on the Petri dish and record the number.
Spread Plate Method: a. Take a Petri dish containing solid agar medium. b. Take a sample from a specific dilution and place it on the surface of the agar. c. Spread the sample evenly over the agar surface using a sterile spreader or a glass rod. d. Allow the agar to solidify. e. Incubate the Petri dish at suitable conditions for the growth of the target bacteria. f. Count the resulting colonies on the Petri dish and record the number.
Calculation: Calculate the number of colony-forming units (CFUs) per milliliter (CFU/mL) of the original culture based on the number of colonies counted and the dilution factor. Multiply the average colony count by the dilution factor to obtain the CFU/mL value.

pour plate method | Image Source: https://courses.lumenlearning.com

spread plate method | Image Source: https://courses.lumenlearning.com

3. Most Probable Number (MPN)

(The MPN method is a statistical procedure used to estimate the number of bacterial cells in a sample, particularly when they cannot be detected using the plate count method. It involves inoculating multiple tubes or wells with different dilutions of the sample and observing growth or lack of growth after incubation. By referring to MPN tables or using software, the most probable number of cells can be determined based on the pattern of positive and negative growth.)

The most probable number (MPN) method is a statistical procedure used to estimate the number of viable microorganisms in a sample, particularly in dilute samples where the number of microorganisms is too low to be detected by plate count methods. It is commonly employed in the analysis of water and food samples. The MPN method relies on observing detectable growth indicators such as changes in turbidity or color due to metabolic activity.
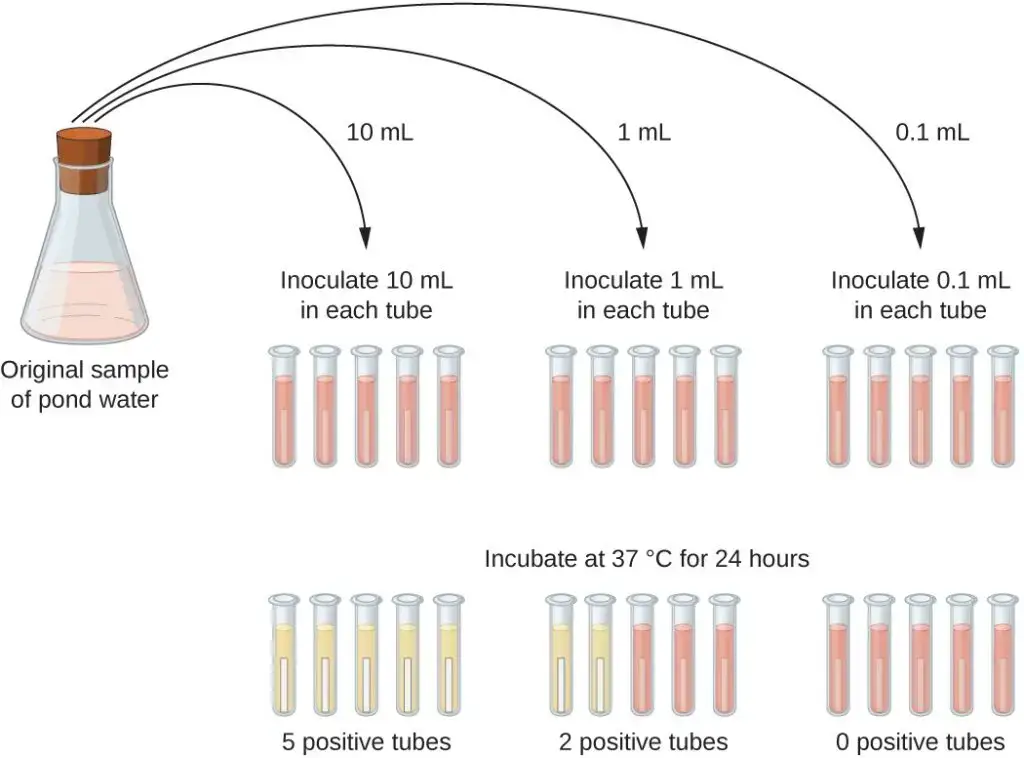
One practical application of the MPN method is in estimating the number of coliforms in a sample of pond water. Coliforms are gram-negative rod bacteria that ferment lactose and their presence in water is an indication of fecal contamination. To determine the MPN, a series of three dilutions of the water sample are prepared. For each dilution, multiple lactose broth tubes are inoculated with different volumes of the sample: 10 mL, 1 mL, and 0.1 mL. The lactose broth tubes contain a pH indicator that changes color from red to yellow when lactose fermentation occurs.
After inoculation and incubation, the tubes are examined for color changes indicating coliform growth. In this specific example, the first set of tubes (10 mL sample) shows growth in all the tubes, the second set (1 mL sample) shows growth in two out of five tubes, and the third set (0.1 mL dilution) shows no growth in any of the tubes. These observations are then compared with a table, such as “Figure 1 in Mathematical Basics,” which is constructed based on a probability model of the sampling procedure.
From the comparison with the table, the most probable number of bacteria per 100 mL of pond water is determined. In the given scenario, the numbers 5, 2, and 0 are evaluated, and the table suggests that the most probable number of bacteria per 100 mL of pond water is 49.
The MPN method provides an estimation of microbial numbers based on statistical probabilities, offering a useful approach when plate count methods are not suitable due to low microorganism concentrations. It is widely used in microbiology for assessing microbial contamination in various samples, including water and food.

most probable number method | Image Source: https://courses.lumenlearning.com

Procedure

The Most Probable Number (MPN) method involves a series of steps to estimate the number of viable microorganisms in a sample. Here are the general steps of the MPN method:

Prepare a series of dilutions: Start by preparing a series of dilutions of the sample. Typically, three dilutions are used, but the number may vary depending on the specific requirements. The dilutions should cover a range that allows for the detection of microbial growth.
Inoculate multiple tubes: Inoculate multiple tubes with each dilution. For each dilution level, multiple replicate tubes are inoculated to increase the accuracy of the estimation. The exact number of tubes depends on the statistical significance required for the analysis.
Use suitable growth medium: Select a suitable growth medium for the microorganisms of interest. The medium should support their growth and provide a detectable indicator of microbial activity or growth, such as a color change or turbidity.
Incubate the tubes: Incubate the tubes at an appropriate temperature and for a suitable duration to allow for the growth of microorganisms. The incubation conditions depend on the specific microorganisms being targeted.
Examine for growth indicators: After the incubation period, examine each tube for the presence of growth indicators. These indicators could include changes in color, turbidity, or other visible signs of microbial activity. Record the presence or absence of growth for each tube.
Interpret the results: Compare the growth observations with a statistical table or MPN chart that provides the probability of microbial presence based on the observed results. This table is constructed using mathematical models and statistical calculations.
Determine the MPN: Based on the comparison with the statistical table, determine the most probable number (MPN) of microorganisms in the original sample. The MPN is the estimate of viable microorganisms per unit volume, such as per milliliter or per gram.

4. Indirect Cell Count

(This method measures the cell density of a culture indirectly by assessing the turbidity or optical density of a liquid suspension. A spectrophotometer is commonly used to measure the absorbance of light passing through the sample. The more turbid or opaque the culture, the higher the absorbance or optical density, which correlates with a higher cell density. This method provides a quick and easy estimation of bacterial growth but does not distinguish between viable and non-viable cells.)

The indirect cell count methods are alternative approaches used to estimate and compare cell densities in a culture without directly counting the cells. Two commonly used indirect methods are measuring turbidity and measuring dry weight. Here’s an explanation of each method:

(a) A spectrophotometer, (b) A spectrophotometer works by splitting white light from a source into a spectrum. | Image Source: https://courses.lumenlearning.com

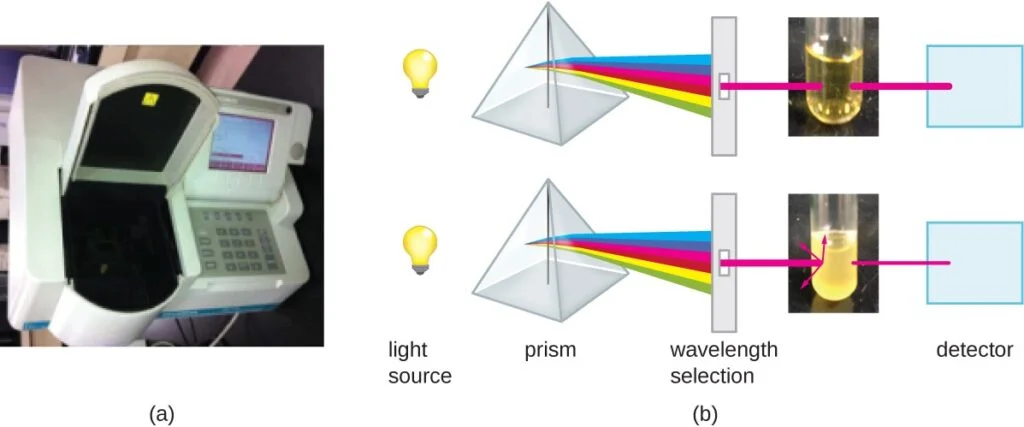
Turbidity Measurement: Turbidity measurement is based on the principle that as the number of bacteria in a liquid suspension increases, the turbidity or cloudiness of the sample also increases. This method utilizes a laboratory instrument called a spectrophotometer. In a spectrophotometer, a light beam is transmitted through a bacterial suspension, and the amount of light passing through the sample and reaching a detector is measured. The measurement is typically expressed as either percent transmission or absorbance (optical density), which is a logarithmic value. When there are more bacteria in the suspension, less light passes through, resulting in a decrease in percent transmission and an increase in absorbance.

To correlate turbidity readings to the actual number of cells, a calibration curve is generated. This is done by performing a viable plate count of samples taken from cultures with a range of absorbance values. The calibration curve plots turbidity as a function of cell density. Once the curve is constructed, it can be used to estimate cell counts for other samples obtained or cultured under similar conditions within the range of values used to create the curve.

Dry Weight Measurement: Measuring the dry weight of a culture sample is another indirect method of evaluating cell density. This method is particularly useful for filamentous microorganisms that are difficult to count directly or through viable plate counts. The process involves concentrating the cell suspension through filtration or centrifugation, washing the cells, and then drying the sample. The drying process must be standardized to account for residual water content. Once the sample is completely dry, its weight is measured, providing an estimate of cell density based on the assumption that the dry weight correlates with cell mass.

These indirect methods offer advantages such as speed and ease of implementation. They provide estimates of cell density without the need for labor-intensive and time-consuming procedures like direct cell counting or viable plate counts. Additionally, recent advancements have introduced even faster and simpler indirect methods that measure cell activity by monitoring the production of metabolic products or the disappearance of reactants. Examples of such methods include measuring adenosine triphosphate (ATP) formation, protein and nucleic acid biosynthesis, and oxygen consumption, all of which can be used to estimate cell numbers.

Procedure

The steps involved in an indirect cell count method, such as measuring turbidity or dry weight, can vary depending on the specific technique and equipment used. However, here is a general outline of the steps involved in an indirect cell count:

Sample Preparation:
- Start with a culture or suspension of cells that you want to estimate the cell density of.
- Ensure the sample is representative and well-mixed to obtain accurate results.
Turbidity Measurement: a. Spectrophotometer Method:
- Set up the spectrophotometer according to the manufacturer’s instructions.
- Select an appropriate wavelength for the measurement, typically one that corresponds to the maximum absorption of the sample.
- Calibrate the spectrophotometer using a blank or control sample (usually the growth medium without cells) to zero the instrument.
- Measure the turbidity of the cell suspension by placing it in a cuvette and inserting it into the spectrophotometer.
- Record the percent transmission or absorbance reading obtained from the spectrophotometer.
Calibration (Turbidity Method):
- Prepare a series of samples with known cell densities by performing viable plate counts on dilutions of the original culture.
- Measure the turbidity of each of these samples using the spectrophotometer.
- Plot a calibration curve by correlating the turbidity readings with the corresponding cell densities obtained from the plate counts.
Cell Density Estimation (Turbidity Method):
- Take a sample with an unknown cell density.
- Measure its turbidity using the spectrophotometer.
- Refer to the calibration curve to estimate the cell density based on the corresponding turbidity reading.
Dry Weight Measurement:
- Concentrate the cell suspension by filtration or centrifugation to obtain a pellet of cells.
- Wash the pellet with an appropriate solution to remove any contaminants or residual media.
- Dry the washed cells using methods such as air drying, lyophilization (freeze-drying), or desiccation.
- Weigh the dried cells using a balance, ensuring the weight measurement is accurate and reproducible.
Analysis and Calculation:
- Once you have obtained the turbidity reading or dry weight measurement, perform any necessary calculations or conversions to estimate the cell density.
- If using turbidity, refer to the calibration curve to convert the turbidity reading to cell density.
- If using dry weight, apply the appropriate conversion factors or known correlations between dry weight and cell mass to estimate the cell density.

Growth Rate and Generation Time

The growth rate and generation time of bacteria are important parameters that describe their reproductive capabilities. The growth rate refers to the speed at which a bacterial population increases in number during the exponential growth phase. It is commonly measured by determining the doubling time or generation time of bacteria. The generation time is the time it takes for the population to double in size.

Under standard nutritional conditions, including the culture medium, temperature, pH, and other factors, bacterial growth rates vary, leading to different generation times. The generation time can range from as short as 12 minutes to as long as 24 hours or more, depending on the species and environmental conditions.

For example, in the laboratory, Escherichia coli, a commonly studied bacterium, has a generation time of 15-20 minutes. However, in the intestinal tract, the generation time of coliform bacteria like E. coli is estimated to be 12-24 hours. Most cultured bacteria have generation times ranging from approximately 15 minutes to 1 hour.

Certain bacteria, such as symbionts like Rhizobium and lithotrophs like nitrifying bacteria, tend to have longer generation times compared to others. Pathogenic bacteria like Mycobacterium tuberculosis and Treponema pallidum have particularly long generation times, which is believed to contribute to their virulence.

The generation times of various bacteria under optimal growth conditions are listed in below:

Escherichia coli: 17 minutes (Glucose-salts medium)
Bacillus megaterium: 25 minutes (Sucrose-salts medium)
Streptococcus lactis: 26 minutes (Milk)
Streptococcus lactis: 48 minutes (Lactose broth)
Staphylococcus aureus: 27-30 minutes (Heart infusion broth)
Lactobacillus acidophilus: 66-87 minutes (Milk)
Rhizobium japonicum: 344-461 minutes (Mannitol-salts-yeast extract medium)
Mycobacterium tuberculosis: 792-932 minutes (Synthetic medium)
Treponema pallidum: 1980 minutes (Rabbit testes medium)

These values provide insights into the relative growth rates and generation times of different bacterial species under specific growth conditions. Understanding the growth rate and generation time of bacteria is important for various applications, including microbial ecology, industrial processes, and the development of treatment strategies against bacterial pathogens.

Calculation of Generation Time

To calculate the generation time of bacteria, you can use the following formula based on the exponential growth pattern of binary fission:

G (generation time) = t/n

Where: G = Generation time t = Time interval in hours or minutes n = Number of generations (number of times the cell population doubles during the time interval)

To calculate the number of generations, you can use the formula:

n = logb – logB log2

Where: n = Number of generations b = Number of bacteria at the end of the time interval B = Number of bacteria at the beginning of the time interval

To solve for n, you can rearrange the equation as:

n = 3.3 logb/B

Once you have determined the number of generations, you can substitute it back into the generation time formula to calculate the generation time (G):

G = t/n

Solving for G gives:

G = t / (3.3 log b/B)

By plugging in the appropriate values for t, b, and B, you can calculate the generation time of the bacterial population. This calculation allows you to determine the time it takes for the population to double and provides insights into the reproductive capabilities of the bacteria under specific conditions.

Example:

Let’s say you have a bacterial culture in which the initial number of bacteria (B) is 100 and after a certain time interval, the number of bacteria (b) increases to 6400. The time interval (t) is 4 hours.

To calculate the generation time (G), we first need to determine the number of generations (n):

n = logb – logB log2

n = log(6400) – log(100) log(2)

n = 3.807 – 2 0.301

n = 3.507 / 0.301

n ≈ 11.62

Now we can calculate the generation time (G):

G = t / n

G = 4 hours / 11.62

G ≈ 0.344 hours

Therefore, in this example, the generation time of the bacterial culture is approximately 0.344 hours, which means that, on average, it takes around 0.344 hours (or approximately 20.6 minutes) for the bacterial population to double under the given conditions.

Significance of the Bacterial Growth Curve

The bacterial growth curve holds significant importance in various fields, both in research and commercial applications. Understanding the growth kinetics and population dynamics of bacteria provides valuable insights and aids in decision-making processes. Here are some key aspects highlighting the significance of the bacterial growth curve:

Utilization and Inoculation: Bacterial growth curves are crucial when it comes to utilizing or inoculating known numbers of bacterial isolates for specific purposes. For instance, in agriculture, understanding the growth curve helps in enhancing plant growth by introducing beneficial bacteria. Similarly, in biodegradation processes, such as the breakdown of toxic organics, knowledge of growth kinetics is essential for optimizing the inoculation of appropriate bacterial strains.
Industrial Production: Bacterial growth kinetics play a vital role in industrial production. By studying the growth curve, scientists and industry professionals can determine the optimal conditions and nutrient requirements for producing antibiotics or other natural products on a large scale. This knowledge helps in maximizing production efficiency and yield.
Substrate Metabolism: Bacterial growth curves are useful for assessing the metabolic capabilities of bacterial strains. By studying the growth kinetics, researchers can determine if specific strains are adapted to metabolize certain substrates. This is particularly valuable in areas such as waste management, where bacteria are engineered to clean up pollutants. Growth curves can indicate whether the bacteria can effectively metabolize industrial waste or oil pollution without being hindered by toxic effects.
Evaluation of Energy Sources: The slope and shape of growth curves obtained from bacteria grown with mixtures of industrial waste products provide insights into their ability to metabolize particular substances. This information helps scientists assess the potential energy sources available in the waste mixture and determine the suitability of specific bacterial strains for waste treatment or bioremediation purposes.

In summary, the bacterial growth curve is a powerful tool that enables researchers and industry professionals to understand the growth kinetics, population dynamics, and metabolic capabilities of bacteria. This knowledge is crucial for optimizing processes, developing sustainable solutions, and utilizing bacteria in various applications, ranging from agriculture to waste management and industrial production.

Mathematical Expression of Bacterial Growth

The growth of bacteria can be mathematically expressed using certain relationships and terms. Here is the mathematical expression of bacterial growth:

Geometric Growth Pattern: Bacterial growth follows a geometric pattern where a single bacterial cell divides into two, then four, six, and so on, indicating exponential growth over generations (x, x^2, x^4, x^6, …, x^n). Here, ‘x’ represents the initial number of cells, and ‘n’ indicates the number of generations.
Mathematical Expression: The relationship between the initial number of cells (N0) and the final number of cells (N) in a bacterial culture can be expressed as:N = N0 x 2^n … (Equation 1)Where: N: Final number of cells N0: Initial number of cells n: Number of generations
Taking the logarithm of both sides of Equation 1, we get:log10 N = log10 N0 + n log10 2
The number of generations (n) can be calculated using the logarithmic expression:n = 3.3 (log10 N – log10 N0)
Important Terms:
- Generation Time (g): It represents the time required for bacteria to double their population. It is denoted by ‘g’ and can be calculated as: g = t/n Where: t: Time taken by an individual bacterium for cell division into two n: Number of generations
- Growth Rate (R): It quantifies the number of generations of bacteria per hour. The growth rate is denoted by ‘R’ and can be calculated as: R = n/t Where: n: Number of generations t: Number of bacterial cell divisions per hour

Understanding these mathematical expressions and terms helps in studying and quantifying the growth dynamics of bacterial populations. It allows researchers to assess the rate of growth, generation time, and growth potential of bacteria under different conditions and environments.

Growth Curve of Continuous Culture of Bacteria

Continuous culture of bacteria is a method used to maintain bacterial populations in a state of exponential growth over extended periods of time. Unlike batch cultures, where nutrients are not replenished, continuous culture systems provide a constant supply of fresh medium to support continuous growth.
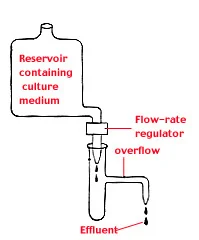
The primary device used for continuous culture is called a chemostat. It consists of a growth chamber connected to a reservoir of sterile medium. The growth chamber is designed to maintain a constant volume of fluid, which is achieved through an overflow drain. The key concept of the chemostat is the controlled addition and removal of medium to regulate bacterial growth.
In a chemostat, the growth process is initiated by introducing bacteria into the growth chamber. Fresh medium is continuously supplied from the reservoir at a rate that limits the growth of the bacteria. This ensures that the bacteria grow at the same rate at which cells and spent medium are removed through the overflow. The addition of fresh medium is carefully regulated to maintain a limiting amount of essential nutrients, preventing nutrient exhaustion and supporting continuous growth.
By providing a constant supply of nutrients and removing excess cells and waste products, the chemostat creates an environment that relieves the conditions that lead to the stationary phase in batch cultures. Nutrient insufficiency, toxic substance accumulation, and excessive cell density, which typically trigger the stationary phase, are controlled in the chemostat. This allows the bacterial culture to be maintained under relatively constant conditions, resembling the growth dynamics of bacteria in natural environments.
The flow rate of nutrients in the chemostat can be adjusted to control the growth rate and maintain a specific bacterial population density. This provides researchers with a versatile tool for studying bacterial physiology, metabolism, and various aspects of microbial ecology. Continuous culture techniques, such as the chemostat, have been instrumental in investigating bacterial growth kinetics, nutrient uptake mechanisms, and microbial interactions in controlled laboratory settings.

Growth Curve of Synchronous Growth of Bacteria

The growth curve of synchronous growth of bacteria refers to the study of bacterial populations in which all cells are at the same stage of the cell cycle. Unlike typical batch or continuous cultures where the distribution of cell size and age is random, synchronous cultures provide valuable insights into the growth behavior of individual bacteria.
To achieve synchronization, various techniques have been developed. These techniques manipulate environmental parameters or use physical methods to select cells that have just completed the process of binary fission. By initiating growth or inducing a growth arrest at a specific point in the cell cycle, researchers can obtain bacterial populations that are synchronized and at the same stage.
When studying synchronous cultures, measurements and observations made on these populations are equivalent to measurements made on individual cells. This allows researchers to examine the growth dynamics, physiological changes, and cellular processes that occur during specific stages of the cell cycle.
In synchronous growth, the smallest cells in the population are those that have recently completed cell division. These cells represent the earliest stage in the cell cycle, and as the culture progresses, the cells gradually increase in size and age. The growth of synchronized cultures is typically illustrated through a growth curve, showing how the population evolves over time.
However, it’s important to note that synchronous cultures rapidly lose synchrony over time. Not all cells in the population divide at exactly the same size, age, or time, leading to variations and loss of synchronization. This is due to inherent biological variability and differences in the growth rates among individual cells.
Despite the limitations of maintaining perfect synchrony, studying synchronous cultures provides valuable information about the growth patterns and dynamics of individual bacterial cells. It enables researchers to investigate cell cycle progression, cellular events associated with specific stages, and the regulation of growth and division processes at the single-cell level. This approach enhances our understanding of bacterial physiology, cell cycle control mechanisms, and the behavior of bacterial populations in response to various environmental conditions.

The synchronous growth of a bacterial population

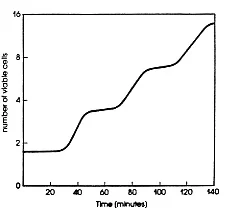
Factors Affecting Bacterial Growth Curve

Nutrient Availability: Bacteria require essential nutrients such as carbon, nitrogen, vitamins, and minerals for growth and reproduction. The availability and concentration of these nutrients in the environment can significantly impact the bacterial growth curve. Limited or inadequate nutrient supply can slow down or halt bacterial growth.
Temperature: Bacteria have an optimal temperature range for growth, and deviations from this range can affect their growth rate. Higher temperatures can denature proteins and inhibit enzyme activity, leading to decreased growth. Lower temperatures can slow down metabolic processes and delay bacterial growth. Each bacterial species has a specific temperature range at which it thrives best.
pH: The acidity or alkalinity of the environment, expressed as pH, influences bacterial growth. Bacteria exhibit different pH requirements depending on the species. Changes in pH can disrupt enzyme activity and cellular processes, affecting growth. Some bacteria prefer neutral pH, while others thrive in acidic or alkaline conditions.
Oxygen: The availability of oxygen in the environment has a significant impact on bacterial growth. Some bacteria require oxygen (obligate aerobes) for their metabolic processes and growth. Others are unable to tolerate oxygen (obligate anaerobes) and may even be harmed by its presence. Additionally, certain bacteria can grow under both aerobic and anaerobic conditions (facultative anaerobes).
Moisture: Adequate moisture is essential for bacterial growth. Bacteria typically require a certain level of water activity (aw) in their environment to carry out metabolic processes. Insufficient moisture can lead to desiccation and inhibit growth, while excessive moisture can create unfavorable conditions or favor the growth of other organisms.
Environmental Factors: Various environmental factors, such as light, pressure, and radiation, can impact bacterial growth. Some bacteria are sensitive to light and can be inhibited by its presence, while others may require specific light conditions for growth. Pressure and radiation can also affect bacterial growth, either inhibiting or promoting it depending on the species and conditions.
Inhibitory Substances: The presence of inhibitory substances, such as antimicrobial agents or toxic compounds, can hinder bacterial growth. Antibiotics, disinfectants, or other chemicals may be present in the environment and can inhibit bacterial growth or even cause cell death.
Competition: Bacterial growth can be affected by competition with other microorganisms for resources and space. In mixed microbial communities, certain bacteria may outcompete others for nutrients, limiting their growth.
Micronutrients: Micronutrients, including trace elements like iron, copper, zinc, and molybdenum, are essential for bacterial growth as they serve as cofactors for enzymatic reactions. Adequate availability of these micronutrients is crucial for bacterial metabolism and growth.
Toxic compounds: Toxic compounds can inhibit bacterial growth or even kill bacteria. Ethanol and other disinfectants are utilized for their antimicrobial properties in disinfection processes. Similarly, toxic compounds can be used in food preservation to hinder the growth of spoilage or pathogenic bacteria.
Genetic Factors: Bacterial growth can be influenced by genetic factors such as the presence of specific genes or genetic mutations. Genetic adaptations can enable bacteria to grow in particular environments or enhance their growth rate under specific conditions.

Applications of Bacterial Growth Curve

Antibiotic Efficacy Testing: The bacterial growth curve is utilized to evaluate the effectiveness of antibiotics and antimicrobial agents. By measuring bacterial growth over time in the presence of different concentrations of an antibiotic, researchers can determine the minimum inhibitory concentration (MIC) required to inhibit bacterial growth. This information helps guide antibiotic treatment strategies and the development of new antimicrobial drugs.
Biotechnology and Industrial Processes: Understanding the bacterial growth curve is crucial in various biotechnological and industrial applications. It helps optimize fermentation processes, such as the production of antibiotics, enzymes, biofuels, and other valuable products. By monitoring and controlling the growth phases, nutrient supply, and environmental conditions, researchers can maximize product yield and quality.
Food Safety and Preservation: Bacterial growth curves are employed in food safety and preservation practices. By studying the growth characteristics of pathogenic bacteria in different food matrices, scientists can identify critical control points to prevent bacterial contamination and ensure food safety. Additionally, the growth curve aids in determining the shelf life and storage conditions for various food products.
Microbial Ecology: The study of microbial communities and their dynamics in different environments relies on the bacterial growth curve. By examining the growth patterns of specific microbial populations, researchers can infer their roles, interactions, and responses to environmental changes. This information contributes to understanding ecosystem processes, bioremediation, and the impact of microbial activities on the environment.
Disease Pathogenesis and Drug Development: The bacterial growth curve provides insights into the pathogenesis of infectious diseases and aids in the development of new therapeutic strategies. By monitoring bacterial growth in host organisms or in vitro models, researchers can identify critical growth stages, evaluate virulence factors, and assess the efficacy of potential drugs or vaccines.
Pharmacokinetics and Drug Dosage: Pharmacokinetic studies involve understanding how drugs are absorbed, distributed, metabolized, and eliminated by the body. Bacterial growth curves assist in determining optimal drug dosage regimens by assessing the drug’s effectiveness in inhibiting bacterial growth over time. This information helps guide dosing schedules and treatment protocols.
Environmental Monitoring and Water Quality: Bacterial growth curves are used in monitoring and assessing water quality and environmental contamination. By analyzing bacterial growth patterns, researchers can evaluate the presence of indicator organisms or pathogens, detect pollution sources, and assess the efficacy of disinfection or treatment methods.

Calculating Number Of Cells

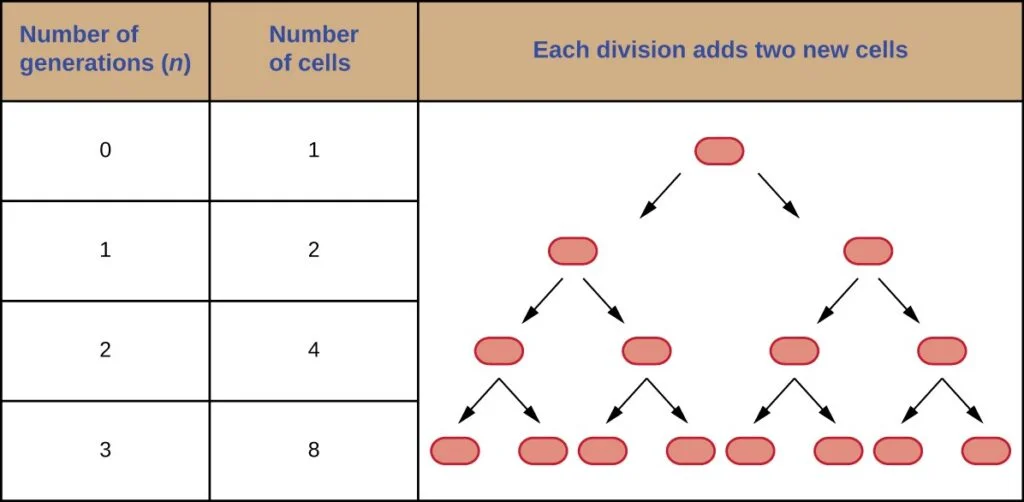
Calculating the number of cells in a population that undergoes binary fission at a constant rate can be done using a simple formula. The formula is based on the exponential increase in cell numbers with each generation.

If cells divide at a constant rate, the number of cells in a population can be expressed as 2^n, where n represents the number of generations. For example, let’s consider a scenario where a single cell divides every 30 minutes for a duration of 24 hours (48 divisions).

Applying the formula 2^n, with n equal to 48, we can calculate that the single initial cell would give rise to 2^48 or 281,474,976,710,656 cells after 48 generations (24 hours). To represent such large numbers more practically, scientific notation is often used. In this case, the number of cells would be expressed as 2.8 × 10^14 cells.

It’s important to note that the formula mentioned above assumes that only one cell is present initially. However, if there are multiple starting cells, the formula can be adapted accordingly. The modified formula becomes:

Nn = N0 × 2^n

Where Nn represents the number of cells at a given generation n, N0 is the initial number of cells, and n is the number of generations.

By applying this adapted formula, one can calculate the number of cells at any generation based on the initial number of cells and the number of generations that have occurred.

Method of Obtaining Bacterial Growth Curve in Laboratory

1. Principle of Bacterial Growth Curve

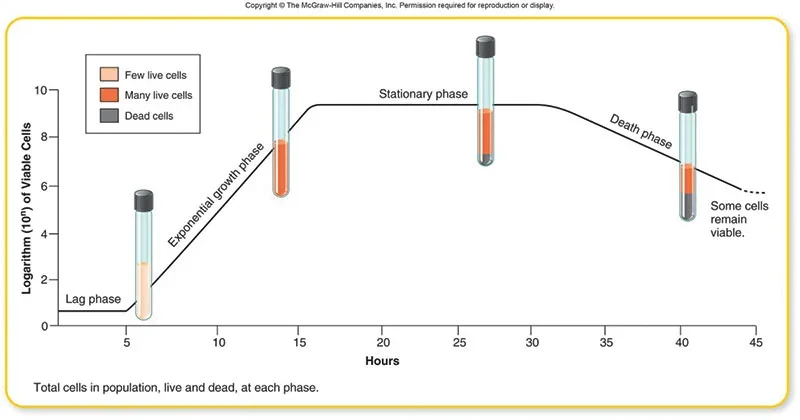
The principle of the bacterial growth curve is a fundamental concept in microbiology that describes the dynamic changes in bacterial population size over time when cultured in a broth medium under optimal conditions. By plotting the increase in cell numbers against the time of incubation, a growth curve is generated, allowing the different stages of the growth cycle to be identified and analyzed.

The growth curve consists of four distinct phases: lag phase, logarithmic (log) phase, stationary phase, and decline or death phase.

Lag phase: In the lag phase, bacterial cells are adjusting to their new environment. During this stage, cellular metabolism is accelerated, leading to rapid biosynthesis of cellular macromolecules, primarily enzymes, in preparation for the next phase of the cycle. Although the cells increase in size, there is no cell division and therefore no increase in the overall cell numbers.
Logarithmic (log) phase: The log phase is characterized by rapid and exponential growth of the bacterial population. Under optimal conditions, with an adequate supply of nutrients and favorable physical conditions, the cells divide by binary fission at a uniform and rapid rate. As a result, there is a regular doubling of the population size, and this doubling time is known as the generation time. The length of the log phase varies depending on the specific organism and the composition of the growth medium. On average, it lasts between 6 to 12 hours.
Stationary phase: In the stationary phase, the growth rate of the bacterial population reaches equilibrium. The number of cells undergoing division is balanced by the number of cells dying. Consequently, there is no net increase in cell numbers, and the population is maintained at its maximum level for a certain period of time. Factors contributing to this phase include the depletion of essential metabolites and the accumulation of toxic acidic or alkaline end products in the medium.
Decline or death phase: The decline phase marks a decrease in the population size due to cell death. The rate of population decrease during this phase closely mirrors the rate of increase observed in the log phase. In theory, the entire population would die within a time interval equal to that of the log phase. However, some highly resistant organisms may persist for an indeterminate length of time, leading to a more gradual decline.

To construct a complete bacterial growth curve, aliquots of the culture are periodically sampled throughout the incubation period. One common method is to measure the turbidity of the culture using spectrophotometry, as it serves as an indicator of increasing cellular mass. The generation time can be determined by extrapolating from the log phase of the curve. Alternatively, the dry cell weight per volume (X) can be used as a measure of cell biomass concentration, providing a convenient alternative to cell number.

In summary, the principle of the bacterial growth curve allows scientists to observe and analyze the growth dynamics of bacterial populations under standardized conditions. This knowledge is crucial in various fields, including microbiology, biotechnology, and medicine, where understanding bacterial growth patterns is essential for research, quality control, and treatment strategies.

Materials Required for Bacterial Growth Curve

To perform a bacterial growth curve experiment, several materials are required to ensure successful cultivation and measurement of bacterial populations. The following are the key materials commonly used in the process:

Bacterial culture: A specific bacterial strain is needed for the growth curve experiment. For example, Escherichia coli (E. coli) is a commonly used bacterium in microbiology studies.
Broth media: Different types of broth media can be used, such as Luria Bertani (LB) broth or Nutrient Broth. These media provide the necessary nutrients for bacterial growth and support the propagation of the bacterial culture.
Glass wares: Various glassware items are essential for preparing and handling the bacterial culture. These include conical flasks, measuring cylinders for accurate volume measurements, sterile test tubes for smaller cultures, and sterile Petri plates for agar-based cultures.
Reagents: Distilled water is required for preparing culture media and dilutions. It is crucial to use sterile distilled water to avoid contamination.
Incubator: An incubator is used to maintain a controlled environment with the optimal temperature for bacterial growth. The temperature may vary depending on the specific bacterial strain being used.
Shaker: A shaker provides continuous agitation to ensure uniform distribution of nutrients and oxygen in the culture medium. It promotes optimal growth conditions by preventing sedimentation of bacterial cells and facilitating aeration.
Spectrophotometer: A spectrophotometer is utilized to measure the optical density (OD) of the bacterial culture. It quantifies the turbidity of the culture, which correlates with the cell density. Spectrophotometric measurements are commonly taken at regular intervals to construct the growth curve.
Micropipettes and tips: Micropipettes are used for accurate and precise measurements of small volumes of liquid, such as adding precise amounts of bacterial culture or reagents to the growth medium. Sterile disposable tips are essential to prevent cross-contamination between samples.
Sterile loops: Sterile loops or inoculation loops are used for transferring and streaking bacterial cultures onto agar plates. They ensure aseptic handling and help in obtaining isolated colonies.

In summary, conducting a bacterial growth curve experiment requires a range of materials including bacterial cultures, suitable growth media, glassware for preparation and cultivation, distilled water, an incubator for temperature control, a shaker for agitation, a spectrophotometer for measuring optical density, micropipettes and tips for precise liquid handling, and sterile loops for inoculation. These materials are vital for creating standardized conditions and accurately measuring the growth of bacterial populations over time.

Procedure of Bacterial Growth Curve

The procedure of the bacterial growth curve involves several steps carried out over the course of three days. The purpose of this procedure is to monitor the growth of bacterial cultures and obtain a growth curve by measuring the optical density (OD) at different time intervals. Here is a step-by-step explanation of the procedure:

Day 1:

Use a sterile loop, and streak a loopful of bacterial culture onto an agar plate. This is done to isolate individual colonies of bacteria.
Incubate the agar plate at 37°C for 18-24 hours to allow the colonies to grow and form visible colonies.

Day 2:

Pick up a single colony of each bacterial strain from the agar plate using a sterile loop and transfer it into a test tube containing 10 ml of autoclaved broth. Each strain should be inoculated into a separate test tube.
Incubate the test tubes overnight at 37°C. This allows the bacteria to grow and multiply in the broth, establishing an overnight culture.

Day 3:

Take 250 ml of autoclaved broth in a sterile 500 ml conical flask. This will serve as the main culture medium for the growth curve experiment.
Inoculate 5 ml of the overnight culture from each test tube into the conical flask containing the broth. Each strain should be inoculated separately.
Take an initial optical density (OD) measurement at zero hour using a spectrophotometer. This measurement provides a baseline for comparison.
Incubate the conical flask at 37°C, allowing the bacterial cultures to grow under controlled conditions.
At regular time intervals (e.g., every 30 minutes), aliquot 1 ml of the culture suspension from the conical flask and transfer it to a separate container.
Measure the optical density (OD) of each aliquot at a wavelength of 600 nm using a spectrophotometer. This measurement indicates the turbidity or density of the bacterial culture, which correlates with cell growth.
Continue taking OD measurements at the specified intervals until the readings become static or reach a plateau. This indicates that the bacterial growth has reached a stationary phase. Alternatively:
Instead of taking OD measurements, you can add 50-100 µl of formaldehyde to each 1 ml aliquot of culture suspension taken after every 30 minutes. This stops the bacterial growth and preserves the samples.
At the end of the experiment, measure the optical density (OD) of all the formaldehyde-treated aliquots using a spectrophotometer.

Finally, to visualize the growth pattern of the bacteria over time, plot a graph with time in minutes on the X-axis and the optical density (OD) at 600 nm on the Y-axis. This graph represents the bacterial growth curve, showing the different phases of bacterial growth (lag phase, exponential phase, stationary phase, and death phase) based on the optical density measurements.

Expected Result of Bacterial Growth Curve

The expected result of a bacterial growth curve is a logarithmic growth curve that represents the changes in the size of a bacterial population over time in a culture. The growth curve exhibits a hyperbolic shape, which is a characteristic of exponential bacterial growth.
Initially, after inoculation, the bacterial population enters a lag phase, during which there is little to no increase in cell numbers as the bacteria adjust to the new environment and prepare for growth. This phase is typically characterized by slow or no growth, as the bacteria acclimate to the culture conditions and synthesize necessary enzymes or adapt to nutrient availability.
Following the lag phase, the bacterial population enters an exponential or logarithmic growth phase. In this phase, the growth rate increases rapidly, and the number of bacterial cells multiplies exponentially. Each bacterial cell divides into two, and these two cells divide again, resulting in an exponential increase in cell numbers. The growth curve during this phase shows a steep upward slope, indicating the rapid proliferation of the bacteria.
As the bacterial population continues to grow, it eventually reaches a stationary phase. In the stationary phase, the growth rate slows down, and the number of cells entering division equals the number of cells dying. As a result, the population reaches a plateau, and the growth curve levels off. Factors such as nutrient depletion, accumulation of toxic waste products, and limited space contribute to the stationary phase.
Finally, if the culture conditions become unfavorable or if the population is subjected to stressors, the bacterial population enters a death phase. During this phase, the number of viable cells decreases, leading to a decline in the overall size of the population. The growth curve exhibits a downward slope as cell death surpasses cell division.
Overall, the expected result of a bacterial growth curve is a hyperbolic logarithmic curve, reflecting the distinct phases of bacterial growth: lag phase, exponential phase, stationary phase, and death phase. The shape of the curve provides valuable insights into the dynamics of bacterial growth and helps in understanding the behavior of bacterial populations in different conditions.

OD Measurement

OD is typically determined by measuring the absorbance of light passing through a bacterial culture using a spectrophotometer. The absorbance is then used as a relative measure of bacterial density.

In the given context, the OD value is adjusted to a standard value of 0.05 using a dilution formula. The formula used is:

OD1V1 = OD2V2

Where:

OD1 represents the initial OD of the broth culture inoculated the previous day.
V1 represents the volume of the broth culture to be added to the inoculum.
OD2 represents the desired OD value (0.05 in this case).
V2 represents the volume of the inoculum (in this experiment, 50 ml).

By substituting the known values into the equation, the value of V1 can be calculated. This calculation determines the volume of the broth culture that needs to be added to the inoculum to adjust its OD to the desired standard.

After adjusting the OD, a portion of the inoculum with a volume of V1 is pipetted out. An equivalent volume of the broth is then added to maintain a constant total volume.

The OD is then checked at regular 30-minute intervals and recorded to monitor the growth of the bacterial culture over time. These recorded OD values are subsequently used to plot a standardized growth curve, with absorbance (OD) on the y-axis and time on the x-axis.

Finally, the generation time can be calculated using the growth curve data. Generation time refers to the time it takes for the bacterial population to double. It can be determined by analyzing the exponential growth phase of the curve and using appropriate mathematical calculations or by estimating the time required for the population to increase by a factor of 2.

Precautions

During the process of conducting a bacterial growth curve experiment, it is important to take certain precautions to ensure accurate and reliable results. Here are some precautions to consider:

Sterile Technique: Maintain strict sterile technique throughout the experiment to prevent contamination. Use sterile equipment, such as loop, test tubes, and conical flasks, and work in a clean and controlled environment.
Proper Incubation: Ensure that the incubation temperature is accurately set and maintained at 37 degrees Celsius to mimic optimal growth conditions for the bacteria being studied. Any deviations in temperature can affect bacterial growth rates and alter the results.
Consistent Sampling: Take samples at regular and consistent time intervals to monitor bacterial growth consistently. Any irregularities in the sampling intervals can introduce variability into the growth curve.
Accurate Measurement: Use precise measuring instruments, such as a spectrophotometer, to obtain accurate optical density (OD) readings. Calibrate the instruments regularly and follow the manufacturer’s instructions for proper usage.
Replicates: Perform the experiment with an appropriate number of replicates to ensure the reliability and reproducibility of the results. Multiple replicates help account for any experimental variations or errors.
Control Group: Include a control group in the experiment, which consists of the growth medium without any bacteria. This control group allows for comparison and helps identify any changes or effects specific to the bacterial cultures being tested.
Data Recording: Maintain thorough and accurate records of all experimental procedures, including culture conditions, sampling times, and measurements. This documentation ensures traceability and facilitates proper analysis of the growth curve data.
Safety Precautions: Adhere to standard laboratory safety protocols, including wearing appropriate personal protective equipment (PPE) such as gloves and lab coats. Dispose of all bacterial waste properly according to the established guidelines.

By following these precautions, researchers can minimize potential errors, maintain data integrity, and obtain reliable results in bacterial growth curve experiments.

Lecture Video

FAQ

What is Generation time? Describe it

Generation time, also known as doubling time, refers to the time interval required for the formation of two daughter cells from a single parent cell. It is a fundamental concept in biology that varies widely among different organisms. In the context of microbial growth, generation time plays a crucial role in determining the rate at which microorganisms multiply.

When conditions are optimal, generation time becomes a key factor in quantitatively analyzing microbial growth. It serves as a unit of measurement for bacterial growth, allowing researchers to understand and compare the reproductive capacity of different bacterial populations.

Suppose we have an initial population of bacteria denoted as No. After one generation, the population (N1) would be equal to 2 times No. Similarly, after the second generation, the population (N2) would be 2 multiplied by 2, or 2^2No. This pattern continues, so after the third generation, the population (N3) would be 2^3No. In general, after the nth generation, the population (Nn) can be calculated as 2^nNo.

Expressing this equation in terms of generation time, we have Nn = 2^nNo. Here, No represents the initial population, Nt represents the population after time ‘t,’ and n represents the number of generations that have occurred after time ‘t.’ Therefore, Nt = No x 2^n.

By taking the logarithm of both sides of the equation, we can derive an expression to calculate the number of generations:

log Nt = log No + n log 2

Using logarithmic identities, we can simplify the equation further:

n = (log Nt – log No) / log 2

This equation allows us to determine the number of generations that have taken place based on the population size at a given time.

The growth rate of a bacterial culture can also be expressed as a factor of the reciprocal of the doubling time. The mean growth rate constant, denoted as k, represents the rate of growth during the exponential phase in a batch culture. It is often expressed as generations per unit time, such as generations per hour.

The equation for the mean growth rate constant is:

k = n / t = (log Nt – log No) / (0.301 t)

Here, t represents the time duration, and k represents the mean growth rate constant.

With the mean growth rate constant, we can calculate the mean generation time or doubling time (g). If the population doubling time is denoted as t = g, the equation becomes:

k = (log Nt – log No) / (0.301 g)

Since Nt is equal to 2No (population doubles during each generation), we can further simplify the equation:

k = log(2No) – log No / (0.301 g)

Using logarithmic properties, the equation becomes:

k = log 2 + log No – log No / (0.301 g)

Simplifying it even more, we find:

k = 1 / g

Therefore, the generation time (g) is equal to 1 divided by the mean growth rate constant (k).

What is a bacterial growth curve?

A bacterial growth curve represents the growth pattern of a population of bacteria over time, typically plotted as the logarithm of the cell count or optical density against time.

What are the phases of a bacterial growth curve?

Bacterial growth curves typically consist of four phases: lag phase, exponential (log) phase, stationary phase, and death phase.

What happens during the lag phase of a bacterial growth curve?

The lag phase is an initial period of adaptation, where bacteria adjust to the environment and prepare for growth. Little to no increase in cell count occurs during this phase.

What characterizes the exponential (log) phase of a bacterial growth curve?

The exponential phase is a period of rapid bacterial growth, where the population size increases exponentially. Cells divide at their maximum rate during this phase.

What occurs during the stationary phase of a bacterial growth curve?

The stationary phase is a plateau phase where the growth rate slows down and the number of dividing cells equals the number of dying cells. Limited nutrients and accumulation of waste products contribute to this phase.

Why does the growth rate stabilize in the stationary phase of a bacterial growth curve?

In the stationary phase, nutrient depletion and waste product accumulation inhibit further cell division, leading to a balance between cell growth and death.

What happens during the death phase of a bacterial growth curve?

The death phase occurs when the number of dying cells exceeds the number of dividing cells. Conditions become unfavorable for growth, and the population size declines.

Can bacterial growth curves differ depending on the bacterial species and environmental conditions?

Yes, bacterial growth curves can vary depending on the bacterial species, nutrient availability, temperature, pH, oxygen levels, and other environmental factors.

How can bacterial growth curves be used in research or industrial applications?

Bacterial growth curves provide insights into microbial physiology, kinetics of growth, and response to environmental conditions. They are used in various fields, including microbiology, biotechnology, food science, and medicine.

What are the applications of bacterial growth curves in antimicrobial research?

Bacterial growth curves help evaluate the effectiveness of antimicrobial agents by monitoring changes in bacterial growth patterns in the presence of different concentrations or combinations of drugs.

References

Zwietering MH, Jongenburger I, Rombouts FM, van ‘t Riet K. Modeling of the bacterial growth curve. Appl Environ Microbiol. 1990 Jun;56(6):1875-81. doi: 10.1128/aem.56.6.1875-1881.1990. PMID: 16348228; PMCID: PMC184525.
Microbiology by Pelczar.
Prescott’s Microbiology by Joanne Willey, Linda Sherwood Adjunt Professor Lecturer, Christopher J. Woolverton Professor.
https://microbeonline.com/typical-growth-curve-of-bacterial-population-in-enclosed-vessel-batch-culture/
https://courses.lumenlearning.com/suny-microbiology/chapter/how-microbes-grow/
https://cran.r-project.org/web/packages/growthcurver/vignettes/Growthcurver-vignette.html
https://biologyreader.com/growth-curve-of-bacteria.html
https://unacademy.com/content/kerala-psc/study-material/general-microbiology/microbial-growth-curve/
https://microbiologynotes.org/bacterial-growth-curve-definition-phases-and-measurement/
https://thebiologynotes.com/bacterial-growth-curve-protocol/
https://biokimicroki.com/bacterial-growth-curve-and-its-application/
https://vlab.amrita.edu/?sub=3&brch=73&sim=1105&cnt=1
https://open.oregonstate.education/generalmicrobiology/chapter/microbial-growth/
https://microbenotes.com/bacterial-growth-curve-and-its-significance/
https://www.uomustansiriyah.edu.iq/media/lectures/6/6_2019_08_06!10_55_17_PM.pdf
https://www.iitg.ac.in/biotech/MTechLabProtocols/Expt-2%20(Specific%20Growth%20Rate).pdf
https://biologyease.com/bacterial-growth-curve/
https://step1.medbullets.com/microbiology/104018/bacterial-growth-curve
https://conductscience.com/bacterial-growth/
https://www.jove.com/v/10511/growth-curves-generating-growth-curves-using-colony-forming-units
https://www.thoughtco.com/bacterial-growth-curve-phases-4172692
http://www2.hawaii.edu/~johnb/micro/medmicro/medmicro.5.html
https://www.tutorialspoint.com/what-are-the-phases-of-the-bacterial-growth-curve
https://theory.labster.com/bacterial-growth-curve/
https://www.onlinebiologynotes.com/bacterial-growth-curve/
https://www.savemyexams.co.uk/international-a-level/biology/edexcel/18/revision-notes/6-microbiology-immunity–forensics/microbiology/6-3-the-bacterial-growth-curve/
https://www.scientificbio.com/blog/what-are-the-stages-of-the-bacterial-growth-curve/

What is Bacterial Growth Curve?

Definition of Bacterial Growth Curve

Binary Fission of Bacteria – Understand the Bacterial Growth

Requirements for Bacterial Growth

Chemical or Nutrient Requirement

Physical Requirements

Phases of Bacterial Growth Curve

1. Lag phase of Bacterial Growth Curve

Lag phase Key Points

2. Log phase or exponential phase

Log phase Key Points

3. Stationary Phase

Stationary Phase Key Points

4. Death Phase

Measurement of Bacterial Growth

1. Direct Cell Count

Procedure

2. Plate Count

Procedure

3. Most Probable Number (MPN)

Procedure

4. Indirect Cell Count

Procedure

Growth Rate and Generation Time

Calculation of Generation Time

Example:

Significance of the Bacterial Growth Curve

Mathematical Expression of Bacterial Growth

Growth Curve of Continuous Culture of Bacteria

Growth Curve of Synchronous Growth of Bacteria

Factors Affecting Bacterial Growth Curve

Applications of Bacterial Growth Curve

Calculating Number Of Cells

Method of Obtaining Bacterial Growth Curve in Laboratory

1. Principle of Bacterial Growth Curve

Materials Required for Bacterial Growth Curve

Procedure of Bacterial Growth Curve

Expected Result of Bacterial Growth Curve

OD Measurement

Precautions

Lecture Video

FAQ

What is Generation time? Describe it

What is a bacterial growth curve?

What are the phases of a bacterial growth curve?

What happens during the lag phase of a bacterial growth curve?

What characterizes the exponential (log) phase of a bacterial growth curve?

What occurs during the stationary phase of a bacterial growth curve?

Why does the growth rate stabilize in the stationary phase of a bacterial growth curve?

What happens during the death phase of a bacterial growth curve?

Can bacterial growth curves differ depending on the bacterial species and environmental conditions?

How can bacterial growth curves be used in research or industrial applications?

What are the applications of bacterial growth curves in antimicrobial research?

References

Related Biology Study Notes

Bacterial Transformation – Definition, Principle, Steps, Examples

Bacterial Conjugation – Definition, Steps, Importance Examples

Bacterial Transduction – Definition, Types, Steps, Examples

Nostoc – Morphology, Life Cycle, Classification, Examples

What are bacteria? – Structure, Metabolism, Size, Shape, Examples

Actinomycetes – Morphology, Classification, Uses

Clostridium perfringens – Habitat, Morphology, Pathogenesis, Treatment

Mycoplasma pneumoniae – Habitat, Morphology, Pathogenesis, Treatment

Latest Questions

Start Asking Questions Cancel reply