Bacterial Growth Curve – Definition, Phases, Factors, Significance

What is Bacterial Growth Curve?

A bacterial growth curve is the graphical representation that shows the increase and decrease in number of bacterial cells in a population with respect to time. It is studied when bacteria are grown in a closed system or batch culture where no fresh nutrients are added and waste products are not removed. Under these conditions the bacterial population shows a typical S–shaped pattern of growth. The growth curve is divided into four phases, namely lag phase, log phase, stationary phase and death phase. In the lag phase the bacterial cells are metabolically active and they synthesize enzymes and other substances but the cell division is not started.

After this the cells enter the log or exponential phase where rapid cell division takes place and the number of bacteria increases very quickly. As nutrients become limited and toxic metabolic products accumulate the growth slows down and the culture enters the stationary phase where the number of new cells formed is equal to the number of cells dying. Finally the death phase occurs when the rate of cell death becomes higher than the rate of cell division and the number of living bacterial cells gradually decreases.

Definition of Bacterial Growth Curve

The bacterial growth curve is a graphical representation of the different phases of bacterial growth over time, including the lag phase, log phase, stationary phase, and death phase.

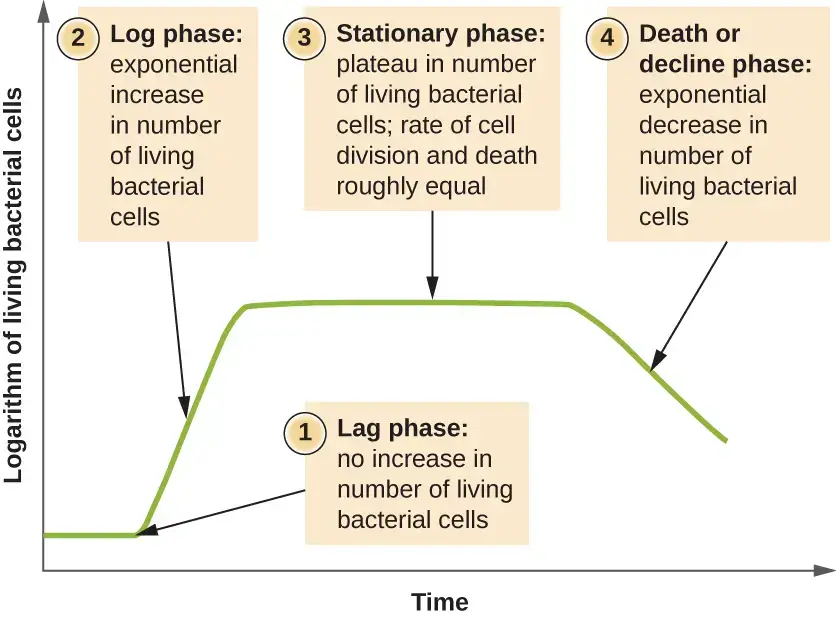
Phases of Bacterial Growth Curve

Some of the main phases of the bacterial growth curve are–

1. Lag Phase– It is the initial stage of the bacterial growth curve. In this phase the bacterial cells are metabolically active but the cells do not divide. The cells increase in size and different enzymes, RNA and metabolites are synthesized which are necessary for the growth of bacteria.
2. Log Phase (Exponential Phase)– It is the phase of active growth. In this phase the bacterial cells divide rapidly and the population increases exponentially. The number of bacterial cells doubles at a constant rate and the growth of bacteria is maximum during this phase.
3. Stationary Phase– In this phase the growth of bacteria becomes constant. The nutrients present in the culture medium become limited and toxic metabolic wastes accumulate in the medium. The number of new cells produced becomes equal to the number of cells dying.
4. Death Phase (Decline Phase)– It is the final phase of the bacterial growth curve. In this phase the environmental conditions become unfavorable for the bacterial cells. The rate of cell death becomes higher than the rate of cell division and the number of living bacterial cells gradually decreases.

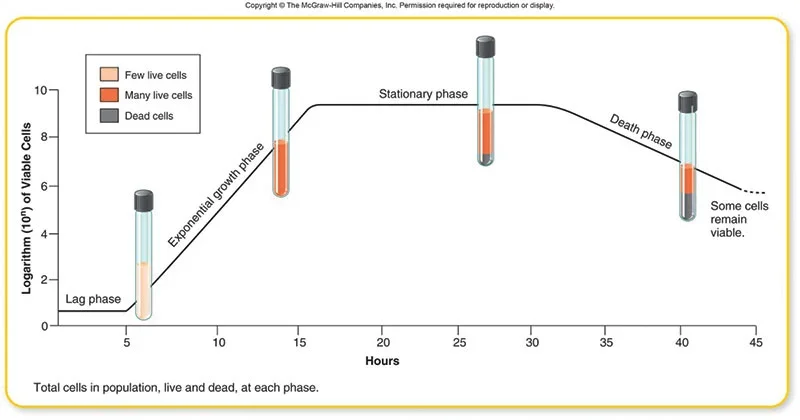
1. Lag phase of Bacterial Growth Curve

Some of the main characteristics of lag phase are–

• It is the initial stage of the bacterial growth curve where the bacterial cells are introduced into a new culture medium.
• In this phase the bacterial cells do not divide and the number of cells remains constant.
• The bacterial cells remain metabolically active during this phase.
• The cells increase in size and become physiologically active.
• Different enzymes, proteins, RNA and other metabolites are synthesized which are necessary for bacterial growth.
• The bacterial cells adapt themselves to the new environmental conditions of the culture medium.
• If the bacterial cells are damaged or injured they repair themselves during this phase before starting cell division.
• The duration of lag phase is variable and it depends on the type of bacteria and the environmental conditions of the culture medium.

2. Log phase or exponential phase

Some of the main characteristics of log phase are–

• It is also referred to as the exponential phase or logarithmic phase of the bacterial growth curve.
• In this phase the bacterial cells divide rapidly by binary fission.
• The number of bacterial cells increases exponentially and the population doubles at a constant rate.
• The bacterial cells show maximum growth and metabolic activity during this phase.
• The cells remain physiologically active and show uniform metabolic activities.
• The bacterial cells synthesize DNA, proteins and cell wall materials actively during this phase.
• The cells are more sensitive to antibiotics and disinfectants during this stage.
• This phase continues only when nutrients are available and environmental conditions such as temperature and pH remain favorable.
• When nutrients become limited and toxic metabolic products accumulate the log phase gradually changes into the stationary phase.

3. Stationary Phase

Some of the main characteristics of stationary phase are–

• It is the phase where the growth of bacterial population becomes constant.
• In this phase the number of new cells formed is equal to the number of cells dying.
• The bacterial population remains stable and no net increase in cell number is observed.
• This phase occurs when the nutrients in the culture medium become limited and space becomes insufficient.
• Toxic metabolic waste products accumulate in the culture medium which affect bacterial growth.
• The metabolic activity of bacterial cells decreases and the cells enter a survival condition.
• Some bacteria may produce secondary metabolites such as antibiotics during this phase.
• Certain bacterial species may form spores to survive under unfavorable environmental conditions.
• The bacterial cells show increased resistance to environmental stress during this phase.

4. Death Phase

Some of the main characteristics of death phase are–

• It is the final stage of the bacterial growth curve.
• In this phase the rate of cell death becomes higher than the rate of cell division.
• The number of living bacterial cells decreases gradually with time.
• This phase occurs due to exhaustion of nutrients in the culture medium.
• Toxic metabolic waste products accumulate in the medium which makes the environment unfavorable for bacterial growth.
• The pH of the culture medium may change which further affects the survival of bacterial cells.
• Many bacterial cells die and may undergo cell lysis releasing their cellular contents into the medium.
• Some bacterial cells may form spores or enter a dormant condition to survive under unfavorable conditions.
• A few bacterial cells may remain viable and survive until favorable environmental conditions return.

Factors Influencing Bacterial Growth Curve

Some of the main factors influencing bacterial growth are–

1. Nutrient Availability– It is the important factor for bacterial growth. Bacteria require nutrients such as carbon, nitrogen, minerals and vitamins for metabolism and cell division. Adequate nutrients support rapid bacterial growth while depletion of nutrients slows the growth.
2. Temperature – Temperature influences the rate of bacterial growth. Each bacterial species grows within a specific temperature range such as psychrophiles, mesophiles and thermophiles. Temperature outside the optimum range slows the growth or may cause death of bacterial cells.
3. pH of Medium– The pH of the culture medium also affects bacterial growth. Most bacteria grow best at neutral pH conditions. Extreme acidic or alkaline conditions inhibit the growth of bacterial cells.
4. Oxygen Availability– Oxygen is an important factor affecting bacterial growth. Some bacteria require oxygen for growth while others grow in the absence of oxygen. Based on oxygen requirement bacteria are classified as aerobic, anaerobic and facultative bacteria.
5. Moisture and Osmotic Pressure– Water availability is necessary for bacterial metabolism and cell division. Low moisture conditions inhibit bacterial growth. The osmotic pressure of the environment also affects the growth of bacterial cells.
6. Light– Light may influence bacterial growth. Certain wavelengths of light such as ultraviolet light can damage bacterial DNA and inhibit bacterial growth.
7. Inhibitory Substances– Certain substances such as antibiotics, disinfectants and toxic chemicals inhibit bacterial growth. Accumulation of toxic metabolic waste products also affects the growth of bacteria.
8. Physical Space– Availability of space in the culture medium influences bacterial growth. In a closed culture system the limited space restricts further cell division and leads to stationary phase.

Significance of Bacterial Growth Curve

Some of the important significance of bacterial growth curve are–

• It helps in determining the generation time or doubling time of bacterial population during growth.
• It helps in predicting and controlling the growth of bacteria under different environmental conditions.
• It provides information about the nutritional and physical requirements of bacterial cells during growth.
• It helps in identifying the exponential phase where bacterial cells are most active and suitable for laboratory experiments.
• It is useful in industrial microbiology for maintaining optimum conditions for bacterial growth during fermentation processes.
• It helps in studying bacterial pathogenesis and the development of infectious diseases.
• It is useful in understanding the mechanism of antibiotic resistance in bacteria.
• It helps in monitoring bacterial growth in food and helps in preventing food spoilage and maintaining food safety.

Lecture Video