Haworth Projection – Definition, Characterisitcs, Examples

What is Haworth projection?

• In the field of chemistry, particularly in organic chemistry and biochemistry, the Haworth projection is a widely used method for representing the cyclic structures of monosaccharides. It provides a simplified three-dimensional perspective, allowing for a better approximation of the actual molecular shape, particularly for furanoses. The projection was named after Sir Norman Haworth, a renowned British chemist who made significant contributions to the study of carbohydrates.
• Monosaccharides are simple sugars that form the basic building blocks of carbohydrates. They consist of a carbon chain with several hydroxyl (-OH) groups and a carbonyl group (C=O). In aqueous solutions, monosaccharides can adopt cyclic structures due to intramolecular reactions between the carbonyl group and one of the hydroxyl groups. These cyclic forms are commonly referred to as pyranoses (six-membered rings) or furanoses (five-membered rings).
• The Haworth projection offers a convenient way to depict these cyclic structures. It utilizes a planar representation of the ring, with the carbon atoms positioned as vertices and the hydroxyl groups indicated as protruding lines. The orientation of these lines above or below the plane of the ring represents the spatial arrangement of the corresponding hydroxyl groups.
• It is important to note that while the Haworth projection provides a useful visual representation, it is an approximation and does not capture the exact conformation of the molecule. For instance, furanoses in reality are nearly planar, whereas the Haworth projection provides a slightly distorted depiction. On the other hand, pyranoses exist in solution primarily in the chair conformation, which is not accurately represented in the projection. Nonetheless, the Haworth projection remains a valuable tool in organic chemistry and biochemistry for its simplicity and ability to convey important structural information.
• Sir Norman Haworth, after whom the projection is named, was a prominent chemist who received the Nobel Prize in Chemistry in 1937 for his investigations into the structures and synthesis of carbohydrates and vitamin C. His work significantly advanced the understanding of the chemistry of carbohydrates, and the Haworth projection stands as one of his enduring contributions to the field.
• In conclusion, the Haworth projection is a commonly used method for representing the cyclic structures of monosaccharides. It offers a simplified three-dimensional perspective and is particularly useful for furanoses. Although it does not precisely reflect the actual conformation of the molecules, it remains a valuable tool in the fields of organic chemistry and biochemistry for visualizing and communicating structural information.

Characteristics of Haworth projection

The Haworth projection is a two-dimensional representation used to depict the three-dimensional structure of cyclic carbohydrates, such as monosaccharides and disaccharides. It provides valuable information about the arrangement of atoms and functional groups within the molecule. Here are some key characteristics of the Haworth projection:

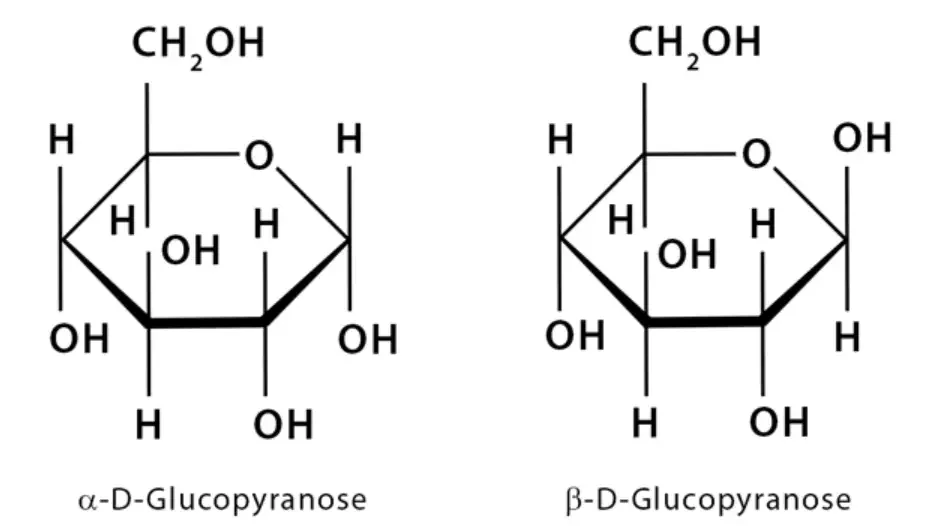
1. Carbon as the implicit type of atom: In a Haworth projection, carbon atoms are represented by a vertex or a corner of the polygonal ring structure. The example usually provided features a hexagonal ring, where atoms numbered from 1 to 6 are all carbon atoms. The carbon atom labeled as 1 is referred to as the anomeric carbon, which plays a significant role in carbohydrate chemistry.
2. Implicit hydrogen atoms: Hydrogen atoms bonded to carbon atoms are not explicitly shown in the Haworth projection. Instead, they are assumed to be present. For example, in the hexagonal ring, atoms 1 to 6 would have additional hydrogen atoms bonded to them, even though they are not depicted in the projection.
3. Thicker lines for atoms closer to the observer: To indicate the relative positions of atoms in space, the Haworth projection employs thicker lines. Atoms that appear closer to the observer are represented with thicker lines, while those farther away have thinner lines. In the hexagonal ring example, atoms 2 and 3, along with their corresponding hydroxyl (OH) groups, would be depicted with thicker lines, signifying their closer proximity to the observer. On the other hand, atoms 1 and 4 would have thinner lines since they are farther away. Atom 5 and the remaining atoms would be represented with the thinnest lines, indicating their furthest position.
4. Relationship to Fischer projection: The groups positioned below the plane of the ring in a Haworth projection correspond to the groups on the right-hand side of a Fischer projection. This rule applies to most of the atoms and functional groups depicted in the Haworth projection. However, there is an exception for the two ring carbons bonded to the endocyclic oxygen atom. The groups attached to these ring carbons do not follow the same orientation as the Fischer projection, but instead have a distinct arrangement specific to the Haworth projection.

The Haworth projection is widely used to represent cyclic carbohydrates and offers a convenient way to visualize their structures. Understanding the characteristics of this projection can aid in interpreting the spatial arrangement of atoms and functional groups within the carbohydrate molecule.

How to Draw a Hayworth Projection?

Drawing a Haworth projection involves several steps to accurately represent the structure of a pyranose or furanose carbohydrate. Here’s a guide on how to draw a Haworth projection:

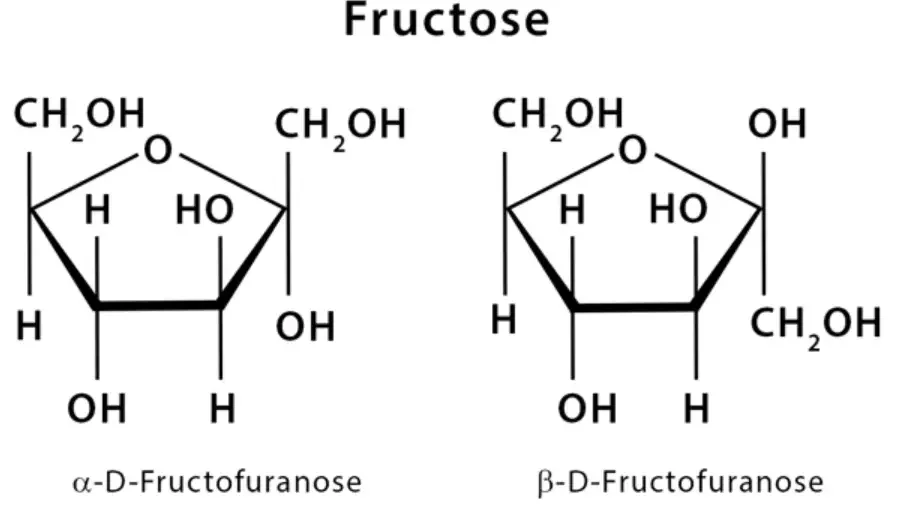
1. Determine the ring size: Identify whether the carbohydrate is a pyranose (6-membered ring) or a furanose (5-membered ring). This information will determine the shape of the polygon to be drawn.
2. Draw the ring: Begin by drawing a flat polygon that represents the ring structure. For a pyranose, draw a hexagon, while for a furanose, draw a pentagon. Ensure that the corners of the polygon are evenly spaced.
3. Place the oxygen atom: Locate the oxygen atom within the ring. In a pyranose, position the oxygen at the upper right corner of the hexagon, and in a furanose, place it at the upper center of the pentagon. This indicates the position of the endocyclic oxygen within the ring.
4. Identify the anomeric carbon: Determine the carbon atom known as the anomeric carbon, which is the hemiacetal carbon at the anomeric position. In most cases, it is placed at the extreme right of the ring. This carbon atom plays a significant role in carbohydrate chemistry.
5. Indicate the bond thickness: To depict the three-dimensional nature of the molecule, differentiate between thicker and thinner bonds. The thicker bonds represent the carbon atoms at the bottom of the ring, which are closer to the viewer. Conversely, the thinner bonds represent the carbon atoms at the top of the ring, which are further away. This distinction helps in understanding the spatial arrangement of the atoms.
6. Vertical bonds for substituents: Attach vertical bonds to the ring to indicate substituents above and below the ring. These vertical bonds are used to represent groups that extend above or below the plane of the ring structure.
7. Representation of hydrogen and hydroxyl bonds: The hydrogen and hydroxyl groups below the ring in the Haworth projection correspond to the groups on the right-hand side of a Fischer projection. To represent these bonds, draw them below the ring structure, corresponding to the right-hand side in a Fischer projection.

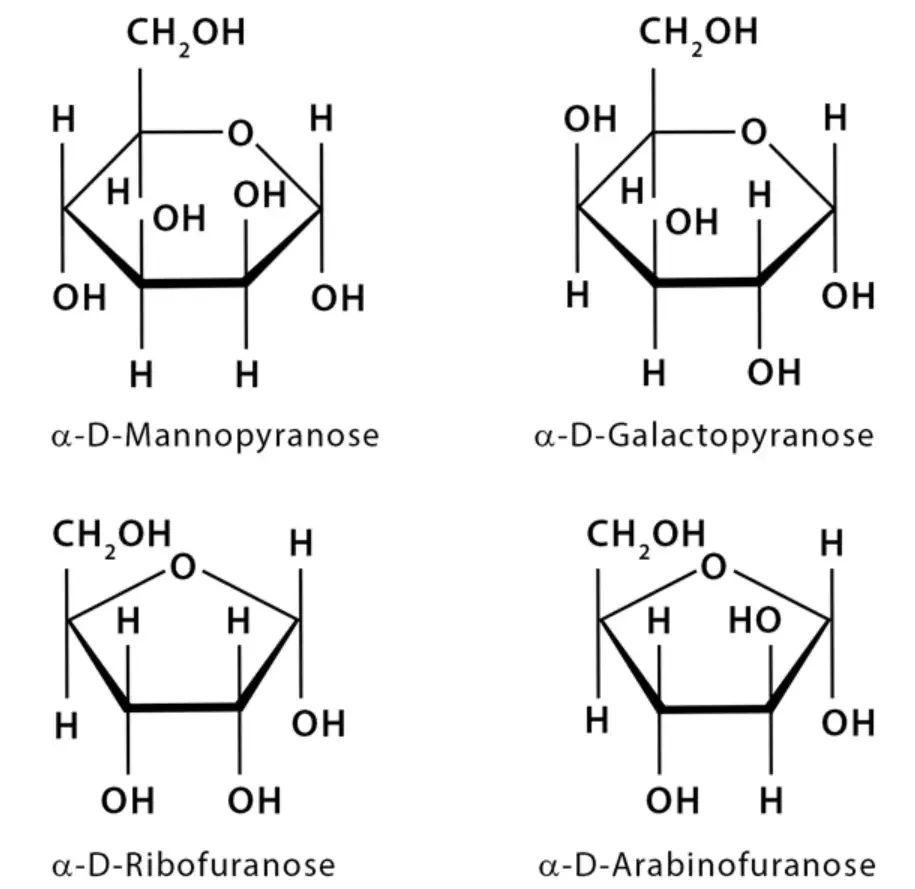
By following these steps, you can draw an accurate Haworth projection that conveys the structural information of a pyranose or furanose carbohydrate. The projection provides a clear visual representation of the molecule’s spatial arrangement, making it easier to understand and analyze its properties.

What is Fischer projections?

The Fischer projection is a widely used method for representing the stereochemical properties and structure of carbohydrates, particularly monosaccharides. Here are some key points about Fischer projections:

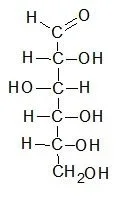
1. Concept and origin: The Fischer projection was developed by German chemist Emil Fischer in 1891, who later received the Nobel Prize in Chemistry in 1902. It provides a clear representation of carbohydrates in their open chain form, as opposed to the cyclic structure depicted in Haworth projections.
2. Vertical and horizontal bond orientation: In a Fischer projection, the carbon atoms forming the main chain of the carbohydrate molecule are represented vertically, while the horizontal bonds depict the connections of hydrogen atoms and hydroxyl groups. The horizontal lines are used to illustrate the bonds that come out of the plane of the projection, whereas the vertical lines represent bonds that are in the plane.
3. Visualization of stereochemistry: Fischer projections offer a distinct advantage in visually identifying the stereochemical properties of carbohydrates. By comparing two Fischer projections, it becomes easy to determine the differences between two carbohydrates, including enantiomers, which are mirror images of each other.
4. Rotation and enantiomerism: Fischer projections can be rotated by 180 degrees without altering the molecule’s stereoisomerism. However, a 90-degree rotation would result in the representation of a different enantiomer. It is important to note that small changes in Fischer projections can significantly impact the characteristics of the molecule, so careful attention must be paid when working with these projections.
5. Limitations and specificity: Fischer projections are primarily used to represent monosaccharides and are particularly useful in carbohydrate chemistry. However, they can be ambiguous and easily confused with other types of drawings. Therefore, their use to represent non-carbohydrates is discouraged. IUPAC recommendations from 2006 also emphasize the explicit representation of hydrogen atoms, especially those at the end group of carbohydrates. Fischer projections should not be confused with skeletal formulas, which have their own conventions.

In summary, Fischer projections provide a straightforward and efficient means of representing the structure and stereochemistry of carbohydrates, especially monosaccharides. Their unique orientation of bonds allows for easy comparison and analysis of different carbohydrates. However, caution should be exercised in their interpretation to avoid confusion and ensure accurate representation.

Steps for Converting Fischer to Haworth

Converting a Fischer projection to a Haworth projection is a straightforward process that involves a few simple steps. Here is a guide on how to convert a Fischer projection to a Haworth projection:

1. Draw the Haworth “stem”: Start by drawing the vertical lines that represent the ring structure of the Haworth projection. The number of vertical lines depends on the size of the ring (e.g., five lines for a pentose or six lines for a hexose).
2. Number the atoms: Number the atoms in the ring from 1 to 5 (or 6) in a clockwise direction, starting from the anomeric carbon (carbon 1). This numbering is essential for accurately placing the substituents in the Haworth projection.
3. Determine the orientation of carbon #6: If the sugar in the Fischer projection is a D-sugar, carbon #6 will be positioned in the “up” direction in the Haworth projection. For an L-sugar, carbon #6 will be oriented “down” in the Haworth projection.
4. Position the “right” groups: In the Fischer projection, identify the groups that are on the right side of carbons 2, 3, and 4. These groups will be placed in the “bottom” positions in the corresponding carbon atoms in the Haworth projection.
5. Position the “left” groups: Similarly, identify the groups that are on the left side of carbons 2, 3, and 4 in the Fischer projection. These groups will be positioned in the “up” positions in the corresponding carbon atoms in the Haworth projection.

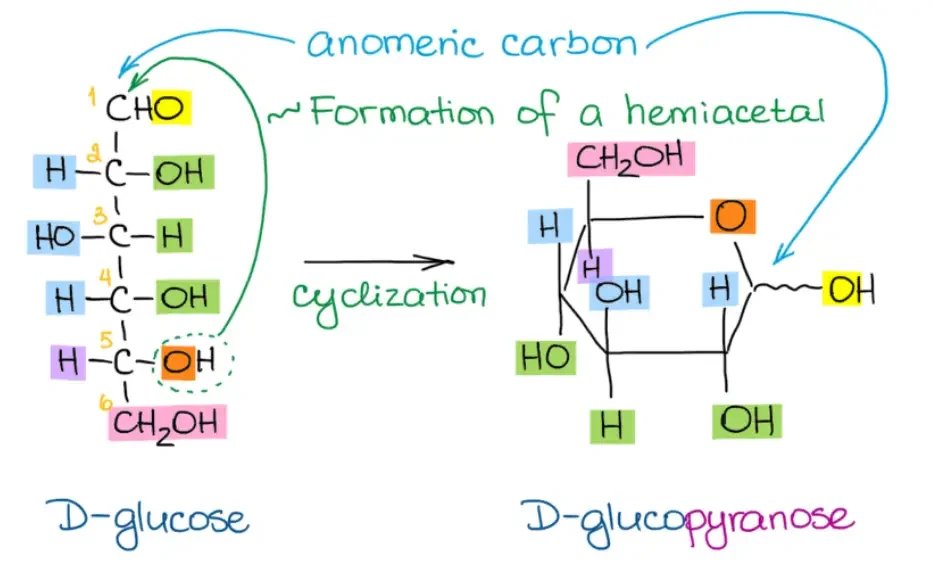
By following these steps, you can convert a Fischer projection into a Haworth projection. With practice, the process becomes more intuitive, and you can accurately represent the cyclic hemiacetal structure of the carbohydrate. Remember to pay attention to the orientation of the substituents and the numbering of the carbon atoms.

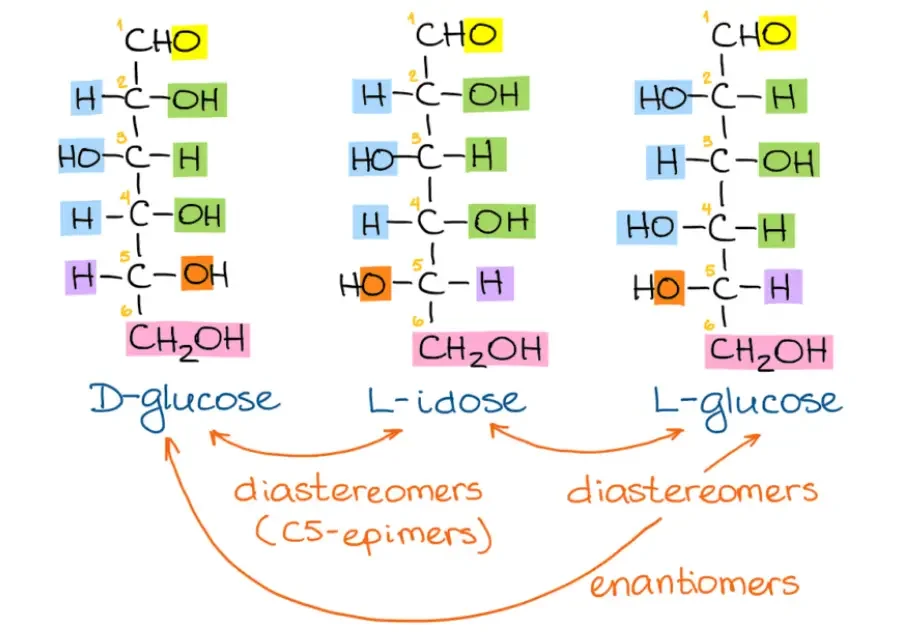
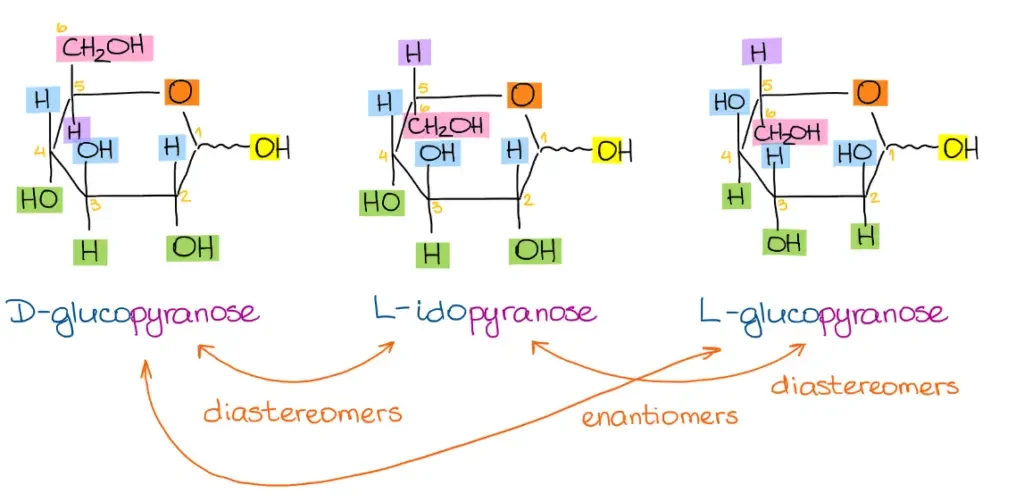
Using these steps, you can convert Fischer projections of various sugars, such as D-glucose, L-idose, and L-glucose, into their corresponding Haworth projections. By practicing the conversion process with different examples, you can become more comfortable and proficient in converting Fischer projections to Haworth projections.

Describe the Haworth projection formulae for glucose

The Haworth projection formula for glucose, a six-carbon aldohexose sugar, is as follows:

          HO
          |
       H - C - OH
          |
    HO - C - H
          |
    HO - C - OH
          |
       H - C - OH
          |
          CH₂OH

In this projection, the vertical lines represent the ring structure, while the horizontal lines represent the bonds that extend out of or into the plane of the projection. The hydroxyl groups (-OH) and hydrogen atoms (-H) attached to the carbon atoms are indicated accordingly. The anomeric carbon, carbon number 1, is the carbon that is bonded to both the oxygen atom of the ring and the -CH₂OH group.

Please note that the Haworth projection represents the cyclic form of glucose, specifically in the α-D-glucopyranose configuration. The configuration (α or β) refers to the orientation of the hydroxyl group attached to the anomeric carbon (carbon 1) in relation to the other carbon atoms.

Haworth projections of maltose

Maltose is a disaccharide composed of two glucose units linked together. The Haworth projection formula for maltose is as follows:

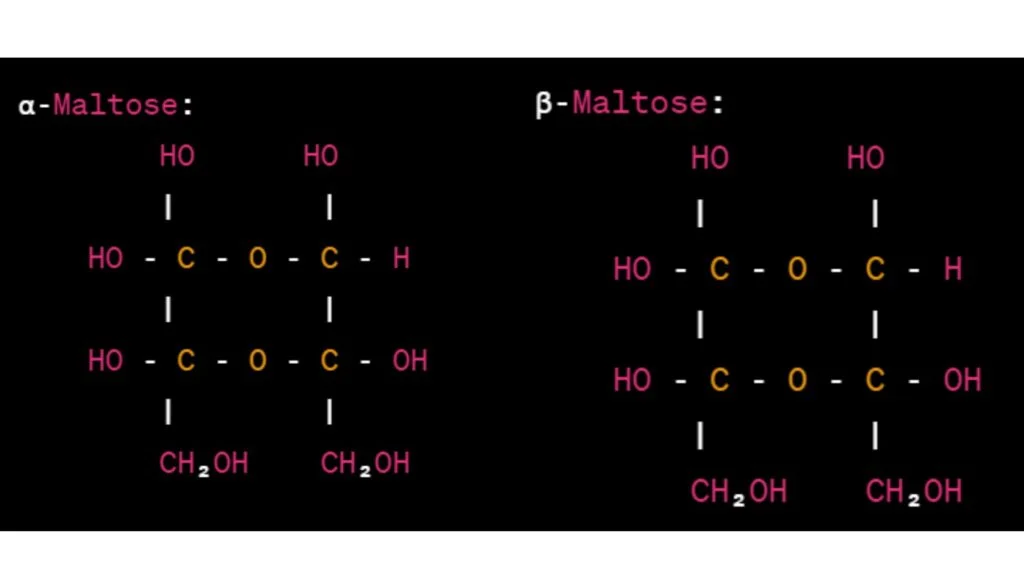
In the Haworth projections above, each glucose unit is represented by a hexagon. The α- and β-maltose configurations differ in the orientation of the glycosidic bond connecting the two glucose units.

In α-maltose, the -OH group attached to carbon 1 of the first glucose unit is below the plane of the ring, while in β-maltose, it is above the plane. The orientation of the glycosidic bond is depicted by the horizontal line connecting the two glucose units.

The hydroxyl groups (-OH) and hydrogen atoms (-H) attached to the carbon atoms are indicated accordingly. The anomeric carbon of the first glucose unit is the carbon bonded to both the oxygen atom of the glycosidic bond and the -CH₂OH group.

These Haworth projections provide a visual representation of the cyclic structure of maltose, highlighting the orientation of the glucose units and the glycosidic bond between them.

Haworth projections of sucrose

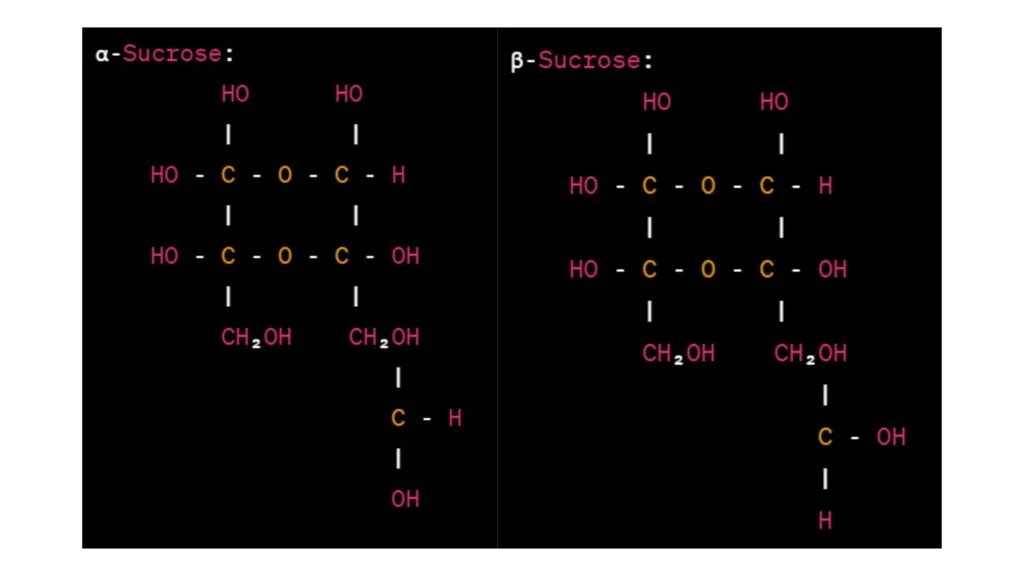
In the Haworth projections above, the glucose unit is represented by a hexagon, and the fructose unit is represented by a pentagon. The α- and β-sucrose configurations differ in the orientation of the glycosidic bond connecting the glucose and fructose units.

In α-sucrose, the -OH group attached to carbon 1 of the glucose unit is below the plane of the ring, while in β-sucrose, it is above the plane. The orientation of the glycosidic bond is depicted by the horizontal line connecting the glucose and fructose units.

The hydroxyl groups (-OH) and hydrogen atoms (-H) attached to the carbon atoms are indicated accordingly. The anomeric carbon of the glucose unit is the carbon bonded to both the oxygen atom of the glycosidic bond and the -CH₂OH group.

These Haworth projections provide a visual representation of the cyclic structure of sucrose, highlighting the orientation of the glucose and fructose units and the glycosidic bond between them.

Haworth projections of lactose

Lactose is a disaccharide composed of one glucose unit and one galactose unit linked together. The Haworth projection formulas for lactose are as follows:

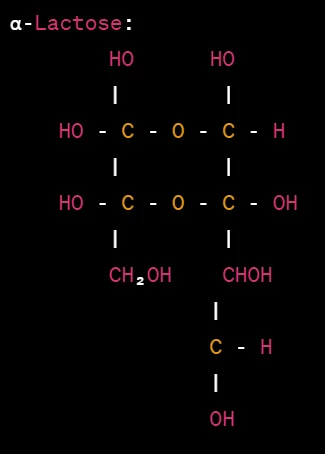
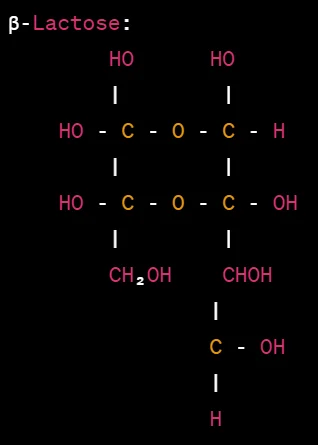
In the Haworth projections above, the glucose unit is represented by a hexagon, while the galactose unit is represented by a pentagon. The α- and β-lactose configurations differ in the orientation of the glycosidic bond connecting the glucose and galactose units.

In α-lactose, the -OH group attached to carbon 1 of the glucose unit is below the plane of the ring, while in β-lactose, it is above the plane. The orientation of the glycosidic bond is depicted by the horizontal line connecting the glucose and galactose units.

The hydroxyl groups (-OH) and hydrogen atoms (-H) attached to the carbon atoms are indicated accordingly. The anomeric carbon of the glucose unit is the carbon bonded to both the oxygen atom of the glycosidic bond and the -CH₂OH group.

These Haworth projections provide a visual representation of the cyclic structure of lactose, highlighting the orientation of the glucose and galactose units and the glycosidic bond between them.

Significance of Haworth Projection

Haworth projections are widely used in the field of carbohydrate chemistry and have several significant advantages and applications:

1. Representation of Cyclic Structure: Haworth projections provide a clear and concise representation of the cyclic structure of carbohydrates, particularly monosaccharides. They allow for a visual understanding of the spatial arrangement of atoms in the ring form of sugars.
2. Stereochemical Information: Haworth projections enable the easy visualization of stereochemical properties, such as the orientation of substituents around the ring. The vertical and horizontal lines in the projection indicate the bonds extending out of or into the plane of the projection, respectively, providing information about the three-dimensional arrangement of atoms.
3. Comparison and Analysis: Haworth projections make it convenient to compare and analyze different carbohydrates, including their isomers and anomers. By examining the position of substituents and the orientation of functional groups, differences in structure and stereochemistry can be easily identified.
4. Hemiacetal and Glycosidic Bond Representation: Haworth projections allow for the clear depiction of hemiacetal and glycosidic bonds present in carbohydrates. The anomeric carbon, involved in these bonds, is explicitly shown, providing insights into the connectivity and bonding patterns of monosaccharides in disaccharides and polysaccharides.
5. Education and Communication: Haworth projections are commonly used in educational settings to teach carbohydrate chemistry and convey structural information. They provide a standardized representation that facilitates communication and understanding among researchers, students, and professionals in the field.

Overall, the significance of Haworth projections lies in their ability to visually represent the cyclic structure and stereochemistry of carbohydrates, enabling easy comparison, analysis, and communication of complex carbohydrate structures.

FAQ