Beer-Lambert Law – Definition, Derivation, and Limitations

The Beer-Lambert Law is a handy principle used to understand how light interacts with substances, like liquids or gases. Imagine shining a flashlight through a glass of colored water—some of the light gets absorbed, right? This law basically says that the amount of light absorbed depends on three things: how thick the glass is (path length), how concentrated the color is in the water (concentration), and a unique property of the colored substance itself (molar absorptivity). If you double the concentration or use a taller glass, the light dims more because there’s more stuff in its path to soak up the photons. Scientists love this because it lets them measure unknown concentrations in labs—like figuring out how much pollution is in a water sample by seeing how much light it blocks. It’s a go-to tool in chemistry, environmental testing, and even medical diagnostics, making complex measurements feel almost straightforward.

What is Beer-Lambert Law?

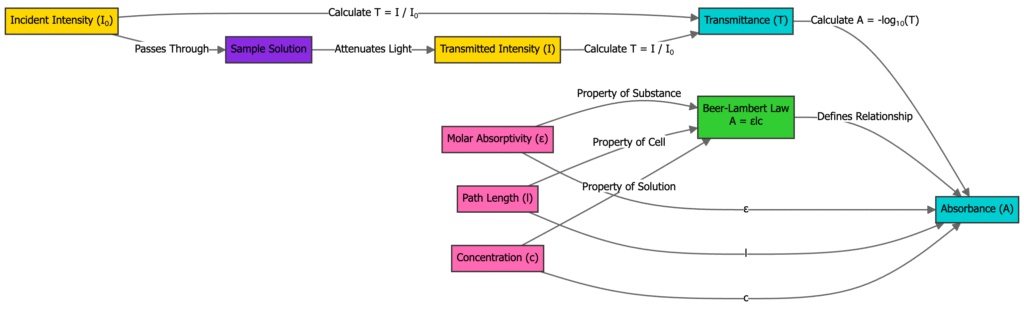
The Beer-Lambert Law is an empirical relationship that describes how the absorbance of light by a homogeneous medium is directly proportional to the concentration of the absorbing species and the optical path length through the medium

The mathematical expression of the Beer-Lambert Law is A = ε ℓ c where A is the absorbance, ε is the molar absorptivity with units L mol⁻¹ cm⁻¹, ℓ is the path length in cm, and c is the concentration in mol L⁻¹

Absorbance A is also defined as the decadic logarithm of the ratio of incident light intensity I₀ to transmitted light intensity I according to A = log₁₀(I₀/I)

The historical development of the Beer-Lambert Law involves three key contributions

• Pierre Bouguer first formulated the relationship between light intensity loss and path length in 1729
• Johann Heinrich Lambert popularized and mathematically expressed this law in his 1760 work Photometria
• August Beer extended the law in 1852 by demonstrating that absorbance is also proportional to solute concentration, completing the modern form of the law

The Beer-Lambert Law is fundamental in UV-Visible and infrared spectrophotometry for quantitative chemical analysis and concentration determination in chemistry, biochemistry, environmental monitoring and medical diagnostics

Key assumptions and conditions for linearity under the Beer-Lambert Law include the following

• The absorbing species act independently without interaction effects
• The medium is optically homogeneous and non-scattering
• The incident radiation is monochromatic or sufficiently narrow in bandwidth
• The light travels as parallel rays each traversing the same path length in the medium

Deviations from linearity can arise due to high analyte concentrations, stray reflections, chemical interactions between absorbing molecules, instrumental factors such as polychromatic light and detector nonlinearity and scattering or turbidity in the solution

The Beer-Lambert Law can be generalized for mixtures with multiple absorbing species as A = ℓ Σᵢ εᵢ cᵢ reflecting the additive nature of absorbance contributions from each species

In practical spectrophotometric measurements standard cuvettes are used with a defined path length typically 1 cm which simplifies calculations and instrument calibration

The molar absorptivity ε is a wavelength-dependent constant specific to each substance and its units are typically L mol⁻¹ cm⁻¹

Modern extensions of the Beer-Lambert Law include variable path length cells for slope spectroscopy which allow concentration determination by varying ℓ instead of c while keeping ε constant

What does beer lambert law state?

The Beer-Lambert Law, also known as Beer’s Law, states that the absorbance of light by a medium is directly proportional to the concentration of the absorbing species and the path length the light travels through the medium.

Mathematically, the law is expressed as:

• A = ε × ℓ × c
  • A is the absorbance (unitless)
  • ε is the molar absorptivity or molar extinction coefficient (L·mol⁻¹·cm⁻¹)
  • ℓ is the path length of the sample (cm)
  • c is the concentration of the absorbing species (mol·L⁻¹)

This relationship assumes that:

• The medium is homogeneous and does not scatter light.
• The absorbing species does not undergo association or dissociation.
• The incident light is monochromatic.

The Beer-Lambert Law is fundamental in spectrophotometry for determining the concentration of substances in solution by measuring light absorbance.

Derivation of Beer-Lambert Law

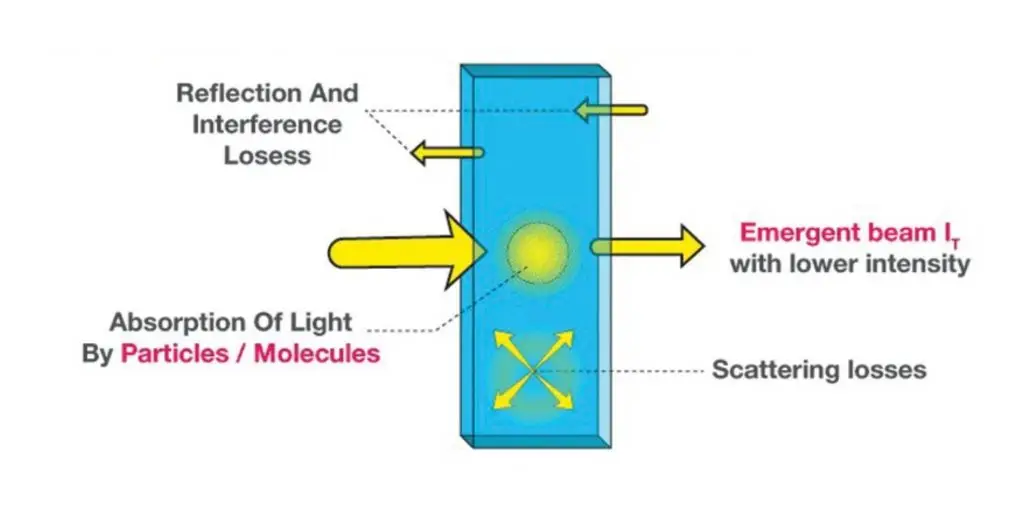
The derivation of the Beer-Lambert Law begins by considering how light intensity decreases as it passes through an absorbing medium.

Step 1: Define the differential change in intensity

When a monochromatic light beam of initial intensity I₀​ enters a medium, a small fraction of it is absorbed over an infinitesimal thickness dx.

The decrease in light intensity dI is proportional to the current intensity I and the infinitesimal path length dx.

This is expressed as:

dI = – αI dx

Where α is the absorption coefficient (cm⁻¹), indicating how strongly the medium absorbs light.

Step 2: Separate and integrate the variables

Rearranging the equation:

dI​/I =−α dx

Integrate both sides:

This gives:

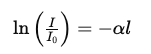
Step 3: Solve for transmitted intensity

Exponentiate both sides:

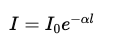
This exponential form describes how light attenuates through the medium.

Step 4: Relate absorption coefficient to concentration

The absorption coefficient α is proportional to the concentration c of the absorbing species and its molar absorptivity ε:

α=εc

Substituting into the equation:

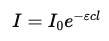
Step 5: Define absorbance

Absorbance A is defined as:

Since:

Conclusion

The final form of the Beer-Lambert Law is:

A=εcl

This shows that absorbance is directly proportional to both the concentration ccc of the absorbing species and the path length lll through which the light travels.

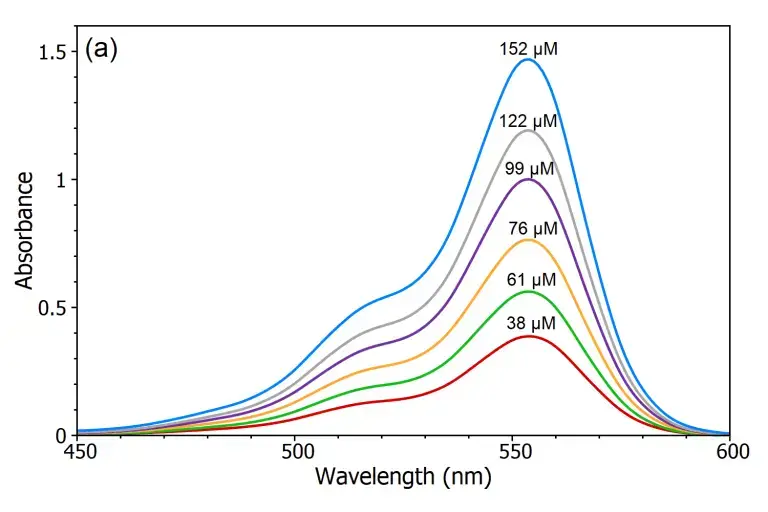
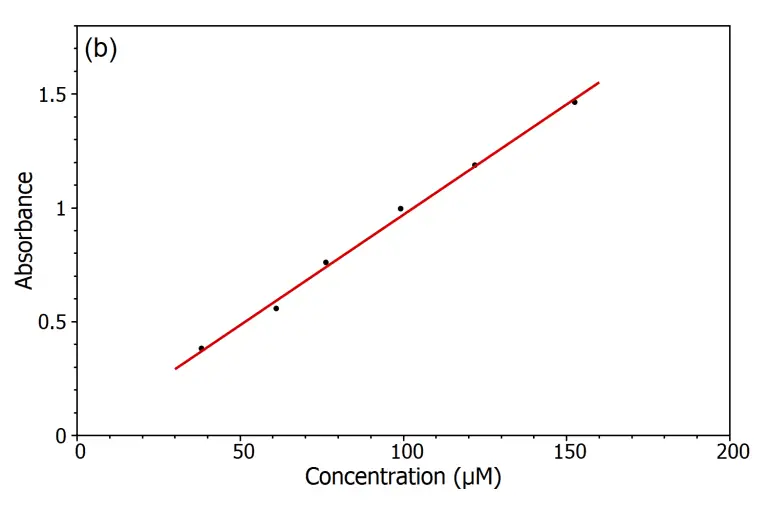
Verification of Beer-Lambert Law

• Prepare a standard 0.1 M aqueous KMnO₄ solution to serve as the stock solution.
• From the stock solution, prepare five different concentrations of KMnO₄ solutions (e.g., 0.0001 M, 0.00025 M, 0.0005 M, 0.00075 M, and 0.001 M).
• Turn on the computer and the instrument power; allow 30 minutes for the instrument to warm up.
• Calibrate the colorimeter or spectrophotometer using a blank solution (distilled water) to set the baseline absorbance to zero.
• Measure the absorbance of each KMnO₄ solution at the wavelength corresponding to the maximum absorbance (λmax) for KMnO₄, typically around 525 nm.
• Record the absorbance values for each concentration.
• Plot a graph of absorbance (A) versus concentration (C) for the KMnO₄ solutions.
• Analyze the graph to determine if a linear relationship exists between absorbance and concentration, which would confirm the validity of the Beer-Lambert law.
• If a linear relationship is observed, use the slope of the line to calculate the molar absorptivity (ε) using the Beer-Lambert equation: A = εlc, where l is the path length of the cuvette.
• Use the established calibration curve to determine the concentration of an unknown KMnO₄ solution by measuring its absorbance and interpolating the corresponding concentration from the graph.

Requirements for Beer-Lambert’s law

• The attenuators must act independently of each other
• The attenuating medium must be homogeneous in the interaction volume
• The attenuating medium must not scatter the radiation—no turbidity—unless this is accounted for
• The incident radiation must consist of parallel rays, each traversing the same path length in the absorbing medium
• The incident radiation should preferably be monochromatic or have a spectral width narrower than that of the absorbing transition
• The incident flux must not influence the atoms or molecules; it should only act as a non-invasive probe, avoiding optical saturation or pumping
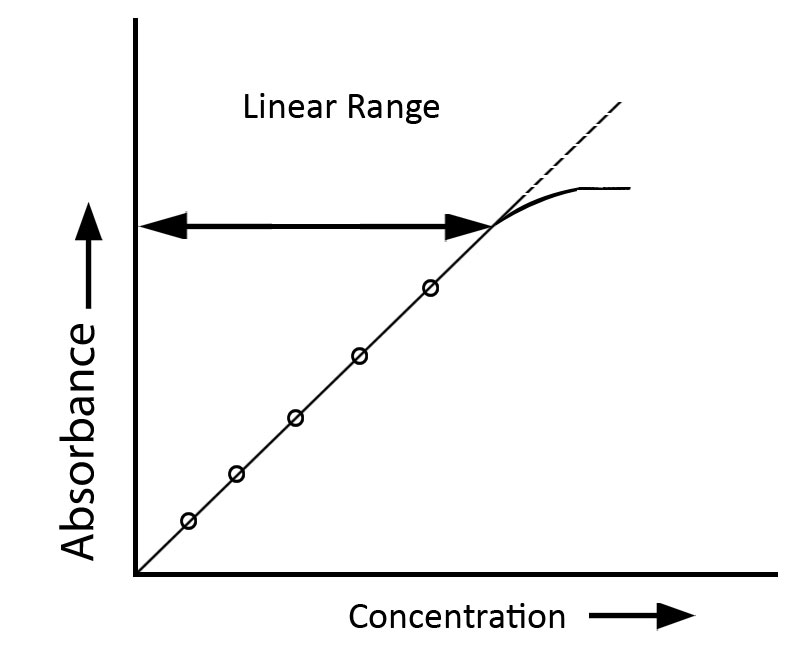
• Absorbance values should ideally fall within the range of approximately 0.2 to 0.5 to maintain linearity under Beer-Lambert conditions

Factors Affecting Beer-Lambert Law

• Concentration of the absorptive species
  • At low concentrations, absorbance is directly proportional to concentration levels.
  • At elevated concentrations (>0.01 M), molecule interactions include electrostatic forces, hydrogen bonding, and aggregation may modify absorptivity, resulting in departures from linearity.
• Path length of the cell of sample
  • Absorbance is directly proportional to the length of the route.
  • Inconsistent or erroneous route length measurements may result in inaccuracies in absorbance estimations.
• Molar absorptivity (ε)
  • This constant is contingent upon the chemical characteristics of the absorbing species and the wavelength of the used light.
  • Alterations in the chemical environment, like pH or solvent polarity, can influence ε, resulting in deviations.
• The incident light’s wavelength
  • The legislation presupposes the utilization of monochromatic light.
  • Utilizing polychromatic light or wavelengths significantly far from the absorption maxima may yield non-linear absorbance responses.
• Instrumental variables
  • Stray light, detector nonlinearity, and light source bandwidth can induce errors.
  • Consistent calibration and upkeep of spectrophotometric apparatus are crucial to mitigate these effects.
• Effects of solvents
  • The polarity of a solvent and its refractive index can affect the absorption properties of solutes.
  • Interactions between solvent and solute may modify the electronic environment of the absorbing species, hence influencing absorbance.
• Chemical equilibrium
  • Changes in concentration of the absorbing species, when involved in a chemical equilibrium, can move the equilibrium position, hence modifying the concentration of the absorbing species and influencing absorbance measurements.
• Temperature
  • Temperature fluctuations can influence the absorptivity and the equilibrium state of processes involving the absorbing species.
  • Ensuring a stable temperature throughout measurements is essential for precise absorbance values.
• Scattering of light
  • Turbid or colloidal solutions can refract light, resulting in apparent absorbance increases that do not correlate with true concentration.
  • Appropriate sample preparation and filtering can reduce scattering effects.
• Fluorescence and phosphorescence
  • If the material exhibits fluorescence or phosphorescence upon light absorption, the released light may interfere with absorbance measurements, resulting in errors.
• Homogeneity of samples
  • The law presupposes a uniform solution.
  • Inhomogeneities, such bubbles or concentration gradients, may result in discrepancies from anticipated absorbance values.
• Variations in refractive index
  • Variations in the refractive index of the solution, particularly at elevated concentrations, might influence the trajectory of light through the sample, resulting in deviations.
• Existence of several absorbing species
  • If many species absorb at the same wavelength, their total absorbance may not be merely additive, particularly if interactions exist among them.
• Photochemical reactions
  • Illumination during measurement may provoke photochemical reactions in some materials, modifying the concentration of the absorbing species and influencing absorbance.
• Limitations of detectors
  • Detectors possess a limited dynamic range.
  • At extreme absorbance values, the detector’s response may exhibit non-linearity, resulting in errors.
• Baseline shift
  • Instrument baselines may shift over time owing to variables such as bulb age or temperature fluctuations, hence impacting absorbance measurements.
  • Consistent baseline adjustments are essential for obtaining precise measurements.

Applications of Beer-Lambert Law 

• Analytical Chemistry – Quantifies concentrations of substances in solutions using spectrophotometry, essential for drug analysis and chemical research.
• Clinical Diagnostics – Measures concentrations of biomolecules like bilirubin in blood samples, aiding in medical diagnoses.
• Environmental Monitoring – Detects and quantifies pollutants in air and water, such as benzene and mercury, ensuring environmental safety.
• Pharmaceutical Quality Control – Ensures the consistency and potency of drugs by analyzing their concentration during manufacturing.
• Food and Beverage Industry– Monitors the concentration of additives and colorants to maintain product quality and compliance with safety standards.
• Microfluidic Devices– Integrates spectrophotometric analysis in lab-on-a-chip systems for rapid, on-site chemical and biological testing.
• Atmospheric Studies – Assesses concentrations of atmospheric gases, contributing to research on ozone depletion and greenhouse gas effects.
• Forensic Science -Determines the concentration of substances in forensic samples, assisting in criminal investigations.
• Chemical Manufacturing– Controls the concentration of reactants and products in industrial processes to ensure product quality and process efficiency.
• Research and Development– Utilized in various scientific studies to analyze the concentration of compounds in experimental samples.

Limitations of Beer-Lambert Law 

The Beer-Lambert Law, which asserts a linear correlation between absorbance and concentration, is constrained by many restrictions that may impact its precision in practical applications.

• At elevated analyte concentrations (often >0.01 M), electrostatic interactions among proximate molecules can modify absorptivity coefficients, resulting in nonlinearity.
• The law presupposes the utilization of monochromatic light; nevertheless, actual light sources frequently emit a spectrum of wavelengths. The existence of non-monochromatic light may induce discrepancies, especially if the absorption spectra fluctuates markedly over the bandwidth.
• The scattering of light by particles in the sample might result in elevated absorbance results, diverging from the anticipated linear correlation. This is especially troublesome in turbid or colloidal liquids.
• The fluorescence or phosphorescence of the sample can produce light, which may be observed in conjunction with transmitted light, resulting in mistakes in absorbance measurements.
• Variations in the refractive index at elevated analyte concentrations might influence the trajectory of light within the sample, hence modifying absorbance measurements.
• Variations in chemical equilibria due to concentration changes might alter the properties of the absorbing species, resulting in discrepancies from the anticipated absorbance.
• Stray light, or light that arrives at the detector without traversing the sample, can induce substantial inaccuracies in absorbance readings, particularly at elevated absorbance levels.
• The rule is typically applicable within low concentration ranges; at extreme high or low concentrations, the linear correlation between absorbance and concentration may not be maintained due to diverse interactions and instrumental constraints.
• The existence of several absorbing species that interact or possess overlapping absorption spectra might complicate the study, resulting in departures from linearity.
• High-intensity light may induce saturation effects or nonlinear detector responses, so compromising the precision of absorbance measurements.
• The rule presupposes that the absorbing species remain chemically unchanged upon light absorption; nevertheless, photochemical processes may modify the concentration of the absorbing species during measurement.
• Temperature differences can influence the absorptivity of the analyte and the refractive index of the solvent, resulting in discrepancies in absorbance measurements.
• Instrumental variables, including detector sensitivity, wavelength accuracy, and route length consistency, can induce mistakes, especially if inadequately calibrated or maintained.
• Inhomogeneities within the sample, like bubbles or concentration gradients, can induce fluctuations in scattering and absorption, resulting in erroneous absorbance readings.
• The presumption of a uniform route length may be invalidated by flaws in the sample container (cuvette) or misalignment of the light beam, so compromising the precision of absorbance measurements.
• The rule does not consider the polarization of light; in instances when the sample displays dichroism, the absorbance may vary based on the polarization state of the input light.
• Chemical reactions or interactions between the analyte and solvent can modify the absorption properties, resulting in variations from the anticipated absorbance.
• The rule presupposes a uniform distribution of the absorbing species within the solution; any aggregation or precipitation may result in non-uniform absorption and dispersion, hence compromising measurement accuracy.
• Background absorption from the solvent or other constituents might disrupt the measurement of the analyte’s absorbance, resulting in errors.
• The rule is less relevant to solid materials or suspensions when scattering and reflection predominate over absorption, necessitating different analytical methods.

Beer lambert law calculator

• https://www.omnicalculator.com/chemistry/beer-lambert-law
• https://www.aatbio.com/tools/quick-calculator/beer-lambert-formula-calculator
• https://www.sigmaaldrich.com/IN/en/support/calculators-and-apps/absorbance-transmittance-conversion
• https://www.calculatorhut.com/chemistry/beer-lambert-law.html
• http://calistry.org/calculate/beerLambertLawAbsorbance
• https://byjus.com/beer-lambert-law-calculator/

Beer-Lambert Law Example Calculation

Q1. Determine the relative amount of light that is absorbed by the sample if the absorbance of the sample is 1 at a specific wavelength.

According to the definition of absorbance;

A = log₁₀ (I₀/I)

The equation is rearranged to determine the relative loss of intensity

10A = I₀/I

10-A= I/I₀

Substituting the value of A = 1

1-I/I₀ = 1 – 10-1 = 1 – 1/10 = 0.9

Therefore, we can say that 90% of the light is absorbed and 10% of light is transmitted.

Q2. Cytosine has a molar extinction coefficient of 6*103 at 270 nm at pH 7. Calculate the absorbance and percent transmission of 1*10-4 and 1*10-3 M cytosine solution in a 1-mm cell. 

Solution

For 1*10^-4M, the absorbance A is given as,

A = log(I₀/I) = e * b * c = 6*10³ * 0.1 * 1*10^-4 = 0.06

in percent transmission, I/I₀ * 100,

A_% = 10^-0.06 * 100 = 10^1.94 (%) = 87.10 %

Similarly, for 1*10^-3M, the absorbance A is given as,

A = log(I₀/I) = e * b * c = 6*10³ * 0.1 * 1*10^-3 = 0.6

in percent transmission, I/I₀ * 100,

A_% = 10^-0.6 * 100 = 10^1.4 (%) = 25.12 %

Q3. A protein with extinction coefficient E1% = 16 yields an absorbance of 0.73 when measured in a 0.5-cm cell. Calculate the weight concentration.

Solution

The absorbance in E^1% can be written as,

A = E^1% * b * c

Where A = 0.73 in a 0.5-cm cell, and = 16. Then, the weight concentration is

c = A / (E^1% * b) = 0.73 / (16*0.5) = 0.091 g/100ml

Q4. Determine the concentration of glycogen-iodine complex if the transmission of light is 40%. Also, the absorption coefficient is 0.20 at 450 nm. The size of the cuvette is 2 cm.

Answer:

Using Beer-Lambert’s law, we know that

-log(It) = -log10(0.4) = (0.20)(c)(2)

c = 0.994

Instrumentation of Beer-Lambert Law

The majority of measurements in experimental research are done using the term transmittance (T) which is described as:

T = I / Io

in which I represents the intensity of light that it reaches after passing through the sample, and Io is the light intensity. The relationship between T and A is:

A = -log T = – log (I / Io).

Absorption of light by a sample;

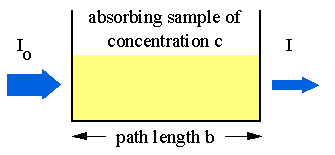
Modern absorption instruments typically display the data in one of three ways: transmittance, %-transmittance or absorbance. A concentration that is not known for an analyte is determined by taking measurements of the quantity of light the sample absorbs, and then employing Beer’s law. If the absorptivity coefficient of the sample is not known, the undetermined concentration can be determined by using the absorption curve against concentration calculated from standards.

FAQ

Q1. What is the reason Beer’s Law is so important?

Beer’s Law is especially important in the areas of physics, chemistry and meteorology. Beer’s Law is used in Chemistry to assess levels of chemicals, to study the rate of oxidation and to determine the degradation of polymers. The law also explains the absorption of radiation by the atmosphere of Earth. Although it is typically used to describe radiation, it aids scientists in understanding what causes the emission of particles like neutrons. In theoretical physics, the Beer-Lambert Law is a solution to the Bhatnagar-Gross-Krook (BKG) operator, which is used in the Boltzmann equation for computational fluid dynamics.

Q2. How can we make use of Beer’s Law?

Many modern instruments can perform Beer’s Law calculations by simply comparing a blank cuvette to the sample, it’s relatively easy to create graphs with standard methods to calculate the amount of substance present in a sample. The method of graphing is based on a straight line relationship between concentration and absorbance, which is applicable for dilute solutions.

Q3. What’s Beer’s Law?

The law of Beer states that the absorbance and concentration have a direct correlation to one their respective levels. This was declared by August Beer.

Q4. What exactly is Lambert Law?

Lambert law states that absorption and length of the path are directly proportional. This was formulated in the work of Johann Heinrich Lambert.

Q5. Why is it that Beer-Lambert law fail in higher concentrations?

Beer-Lambert law is ineffective at higher concentrations due to the fact that the law’s linearity is restricted to instrumental and chemical factors. If the solution is at higher concentrations, the relationship between the molecules in the solution is such that there is a deviation in absorptivity. Additionally as the solution’s concentration gets high the refractive index is altered.