Lotka Volterra equation for competition and Predation

The history of the Lotka-Volterra predator-prey model can be traced back to the early 20th century. Alfred J. Lotka, an American mathematician and biophysicist, first proposed the model in 1910 in the context of autocatalytic chemical reactions. The model was essentially a logistic equation, initially derived by Pierre François Verhulst.

In 1920, Lotka extended the model to “organic systems” with the help of Andrey Kolmogorov, using a plant species and a herbivorous animal species as an example. He further explored predator-prey interactions in his 1925 book on biomathematics. Around the same time, Vito Volterra, an Italian mathematician and physicist, independently published the same set of equations in 1926. Volterra’s interest in mathematical biology was sparked by his interactions with Umberto D’Ancona, a marine biologist studying fish catches in the Adriatic Sea during World War I.

D’Ancona had observed an increase in the percentage of predatory fish caught during the war years, despite reduced fishing efforts. Volterra developed his model to explain this observation, giving credit to Lotka’s earlier work in his publication. As a result, the model became known as the “Lotka-Volterra model.”

Over time, the model was expanded to include density-dependent prey growth and a functional response developed by C. S. Holling. This modified model, known as the Rosenzweig-MacArthur model, provided a more comprehensive explanation of predator-prey dynamics in natural populations.

In the late 1980s, an alternative to the Lotka-Volterra model emerged, known as the ratio-dependent or Arditi-Ginzburg model. This model challenged the assumptions of the traditional model and sparked debates about the validity of prey- or ratio-dependent models in explaining population dynamics.

Beyond biology, the Lotka-Volterra equations have also found applications in economic theory. Richard Goodwin is credited with their initial application in economics in the mid-1960s.

Overall, the Lotka-Volterra predator-prey model has a rich history and has significantly contributed to our understanding of population dynamics in ecological systems and other fields of study.

Lotka–Volterra equations

The Lotka-Volterra equations, also known as the Lotka-Volterra predator-prey model, provide a mathematical description of the interactions between predator and prey populations in ecological systems. These equations are a set of first-order nonlinear differential equations that capture the dynamics of the populations over time.

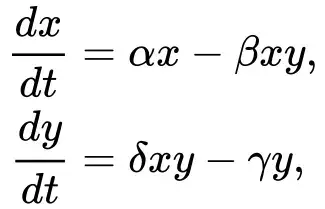
where

• the variable x is the population density of prey (for example, the number of rabbits per square kilometre);
• the variable y is the population density of some predator (for example, the number of foxes per square kilometre);
•  and  represent the instantaneous growth rates of the two populations;
• t represents time;
• The prey’s parameters, α and β, describe, respectively, the maximum prey per capita growth rate, and the effect of the presence of predators on the prey growth rate.
• The predator’s parameters, γ, δ, respectively describe the predator’s per capita death rate, and the effect of the presence of prey on the predator’s growth rate.
• All parameters are positive and real.

The equations represent the changes in population density for the prey (represented by variable x) and the predator (represented by variable y). The prey population density is influenced by its own growth rate (α) and the effect of predator presence on its growth rate (β). The predator population density is influenced by its per capita death rate (γ) and the effect of prey presence on its growth rate (δ).

By solving these equations, one can determine the population dynamics of the predator and prey species. The solutions are deterministic and continuous, assuming that the generations of both species overlap continuously. This means that the population sizes of the predator and prey change in relation to each other over time.

The Lotka-Volterra equations serve as a specific example of the broader Kolmogorov model, which is a general framework for modeling ecological systems with various types of interactions, including predator-prey interactions, competition, disease, and mutualism. The model provides a mathematical foundation for understanding the dynamics and stability of populations in ecological communities.

The Lotka-Volterra equations have been widely used in ecological research and have contributed to our understanding of predator-prey interactions and population dynamics. They help explain phenomena such as population oscillations, cyclical patterns of predator and prey abundance, and the impact of predation on prey populations. These equations have practical applications in fields such as conservation biology, fisheries management, and pest control, where understanding the dynamics of predator-prey relationships is crucial for effective management strategies.

Biological interpretation and model assumptions

The Lotka-Volterra predator-prey model, as described in the previous content, has a biological interpretation and is based on several assumptions about the environment and the biology of the predator and prey populations.

Firstly, the model assumes that the prey population has an unlimited food supply and can reproduce exponentially unless subject to predation. This assumption is represented by the term αx in the prey equation, where α is the maximum prey per capita growth rate. The rate of change in the prey population is determined by its own growth rate minus the rate at which it is preyed upon, which is represented by the term βxy.

Similarly, the model assumes that the growth of the predator population, represented by the term δxy, is proportional to the rate at which it consumes the prey. However, a different constant is used for the predator growth rate compared to the predation rate, as the two rates may not be equal. The term γy represents the loss rate of the predators due to natural death or emigration.

The assumptions of the Lotka-Volterra model include:

1. The prey population always has ample food available.
2. The food supply of the predator population depends entirely on the size of the prey population.
3. The rate of change in population is directly proportional to its size.
4. The environment remains constant throughout the process, without favoring one species over the other, and genetic adaptation is inconsequential.
5. Predators have an unlimited appetite.
6. Both the predator and prey populations can be described by a single variable, assuming no spatial or age distribution that contributes to the dynamics.

These assumptions simplify the model and allow for a more straightforward analysis of the predator-prey dynamics. However, it’s important to note that these assumptions may not hold true in all real-world situations. Ecological systems are often more complex, with multiple factors influencing population dynamics, such as resource limitations, spatial heterogeneity, and age structure.

Despite these assumptions, the Lotka-Volterra predator-prey model provides valuable insights into the general dynamics of predator and prey populations and has been widely used in ecological research. It serves as a foundation for understanding the interactions between species and the factors that influence population fluctuations in biological systems.

Lotka Volterra equation for competition and Predation

The Lotka-Volterra equation is used to interpret population dynamics in which two organisms interact in one of two ways: (a) by competing for shared resources, or (b) by being associated in a prey-predator system.

The equation for the first type of interaction, namely competition for shared resources, is known as the Competitive Lotka-Volterra equations, while the predator-prey equation describes the second type of interaction.

1. Competitive Lotka-Volterra equations

Competitive Lotka-Volterra equations are a mathematical model used to describe the dynamics of two competing species in an ecosystem. These equations are an extension of the traditional Lotka-Volterra equations, which describe the predator-prey relationship between two species. However, in the case of competitive interactions, the equations take into account the effect of competition on the population growth rates.

The Lotka-Volterra equation for competition considers two species, denoted as species 1 and species 2. Each species has its own population size, growth rate, carrying capacity, and competitive effect on the other species. The equations for the population dynamics of species 1 and species 2 are as follows:

dN1/dt = r1N1 [1 – (N1 + a12N1/K1)]

dN2/dt = r2N2 [1 – (N2 + a21N2/K2)]

In these equations, N1 and N2 represent the population sizes of species 1 and species 2, respectively. The growth rates of the populations are represented by r1 and r2, while K1 and K2 denote the carrying capacities of the respective species.

The additional terms in the equations account for the competitive interactions between the two species. The parameter a12 represents the competition coefficient, which quantifies the effect of species 2 on the population growth of species 1. Similarly, a21 represents the competitive effect of species 1 on species 2. If a12 is less than 1, it indicates that species 1 has a greater impact on its own population growth than the effect of species 2. This suggests that intra-specific competition within species 1 is more intense than the inter-specific competition with species 2.

The order in which the populations are represented in the equations indicates the population that is affected by the other population. For example, in the equation for species 1, the competitive effect of species 2 on species 1 is considered. Similarly, in the equation for species 2, the competitive effect of species 1 on species 2 is taken into account.

By solving these equations, ecologists can study the dynamics of competing species in an ecosystem. The model allows them to understand how the populations interact and how competition affects their growth and ultimately their coexistence or competitive exclusion. Analyzing the Competitive Lotka-Volterra equations provides insights into the complex dynamics of species interactions and helps in predicting the outcomes of competition in ecological communities.

Outcomes Interpretation

The outcomes of the Competitive Lotka-Volterra equations can be interpreted based on the values of the competition coefficients (a12 and a21). Here are some interpretations of the outcomes:

1. If a12 = 0, it means that species 1 follows the logistic model of population dynamics. In this case, the growth of species 1 is only influenced by its own population size and carrying capacity, without any competitive effect from species 2.
2. If a21 = 0, it means that species 2 follows the logistic model of population dynamics. Similarly, the growth of species 2 is only affected by its own population size and carrying capacity, without any competitive effect from species 1.
3. If a12 = 1, it indicates strong competition between species 1 and 2. Both species compete with equal magnitude for common resources, implying that the intensity of intraspecific competition within species 1 is equivalent to the intensity of interspecific competition with species 2.
4. If a12 is negative, it suggests that species 2 facilitates resource availability to species 1. In other words, species 2 has a positive effect on the growth of species 1 by making resources more accessible or providing some form of assistance.
5. If both a12 and a21 are negative, it indicates a symbiotic relationship between the two species. In this scenario, the competitive effect is reversed, and the interaction between the species becomes mutually beneficial rather than detrimental.
6. If one of the competition coefficients, either a12 or a21, is zero (0) while the other is negative, it implies a commensalism relationship. The species with the negative competition coefficient benefits from the interaction, while the species with the zero competition coefficient remains unaffected.
7. If one of the competition coefficients is positive and the other has no effect (i.e., zero), it signifies a parasitic relationship. The species with the positive competition coefficient benefits at the expense of the other species, which is not affected by the interaction.
8. If both a12 and a21 have negative values, it indicates competition between the two species. Both species experience a competitive effect on their population growth, suggesting a scenario of resource competition and potential negative impact on the populations.

Interpreting the outcomes based on the signs and magnitudes of the competition coefficients allows ecologists to gain insights into the nature of species interactions and their effects on population dynamics in competitive ecological systems.

2. Lotka Volterra Predation equations

The Lotka-Volterra Predation equations provide a mathematical model to describe the dynamics of predator-prey interactions in biological systems. These equations capture the population growth rates of both the prey and predator species over time.

The equations are represented by a pair of differential equations:

dx/dt = ax – βxy

dy/dt = δxy – γy

In these equations, “x” represents the population size of the prey species, while “y” represents the population size of the predator species. The terms dx/dt and dy/dt represent the growth rates of the prey and predator populations, respectively, with respect to time “t”.

The parameters in the equations have specific meanings:

• The parameter “a” represents the growth rate of the prey population in the absence of predation. It indicates the intrinsic reproductive capacity or the natural growth rate of the prey.
• The parameter “β” represents the predation rate. It quantifies the effect of predators on the reduction of prey population size. The term βxy indicates that the rate of predation is proportional to the product of the prey and predator populations.
• The parameter “γ” represents the natural mortality rate of the predator species. It indicates the rate at which predators die or leave the system in the absence of prey.
• The parameter “δ” represents the efficiency of converting prey into new predator individuals. It quantifies the reproductive success of predators when consuming prey.

By solving these equations, ecologists can analyze the population dynamics of predator and prey species. The equations capture the feedback loop between the two populations, where changes in prey population size influence the predator population size and vice versa.

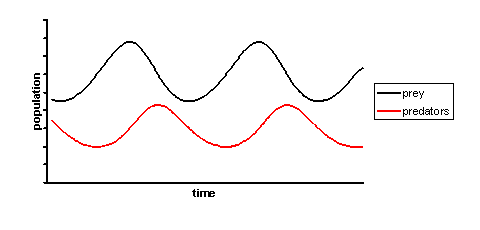
The Lotka-Volterra Predation equations allow for the exploration of various ecological phenomena, such as predator-prey oscillations, population stability, and the impact of predation on prey and predator populations. These equations provide insights into the complex dynamics of predator-prey interactions and help in understanding the factors that influence population sizes and the coexistence or potential extinction of species in ecological communities.

Assumptions

The Lotka-Volterra predation equation is formulated based on several assumptions that simplify the model and provide a framework for understanding predator-prey dynamics. Here are the key assumptions underlying the Lotka-Volterra predation equation:

1. Predators can eat limitlessly: The equation assumes that predators have unlimited access to prey. This assumption implies that there are no constraints on the predator’s ability to capture and consume prey individuals.
2. Food supply depends on prey population size: The availability of food resources, i.e., the prey population, is assumed to be directly linked to the size of the prey population. As the prey population increases, the food supply for predators also increases.
3. Rate of change of population depends on its size: The growth or decline of a population is assumed to be directly proportional to its size. In the Lotka-Volterra predation equation, the rate of change of the prey and predator populations is determined by the size of the respective populations.
4. Constant environment and inconsequential genetic adaptations: The model assumes that the environment remains constant over time, without significant changes. Additionally, it assumes that genetic adaptations within the populations are not considered or have a negligible impact on the dynamics of the predator-prey interaction.
5. Unlimited food supply for prey: The equation assumes that prey have unlimited access to food resources. This assumption implies that there are no factors limiting the growth or survival of the prey population, such as resource depletion or competition within the prey species.

The Lotka-Volterra predation equation is continuous and deterministic, meaning that it assumes a continuous and smooth change in population sizes over time. The equation describes the overlapping dynamics of the prey and predator populations, with the populations interacting and influencing each other’s growth rates.

The rate of growth for the prey population (dx/dt) in the equation is determined by the intrinsic growth rate (a) of the prey population, which represents exponential growth in the absence of predation, minus the rate of predation (βxy), which depends on the interaction between prey and predator populations.

Similarly, the rate of growth for the predator population (dy/dt) is determined by the availability of food resources, represented by the term δxy, minus the decay rate (γy) due to factors such as mortality or emigration. In the absence of prey, the predator population follows an exponential decay.

The solutions to the Lotka-Volterra predation equation are periodic, resulting in oscillations of the prey and predator populations. These oscillations exhibit a simple harmonic motion, where the predator population lags behind the prey population by 90 degrees in each cycle.

While these assumptions simplify the model, they provide a useful framework for understanding the dynamics of predator-prey interactions and can help in predicting population patterns and the coexistence or potential extinction of species in ecological systems.

Functional and numerical responses

Functional and numerical responses are two important concepts in predator-prey dynamics that describe the relationship between prey density and predator behavior or population dynamics.

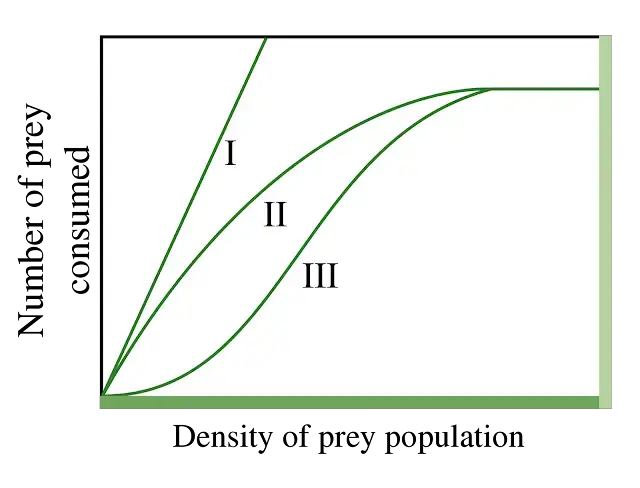
Functional Response: The functional response refers to how the consumption rate of predators changes in response to variations in prey density. There are three types of functional response curves:

1. Type I Response Curve: This type of response curve is rare in nature and is typically observed in filter feeders. It shows a linear relationship between prey density and the rate of consumption by the predator until reaching a saturation point where the predator cannot consume prey any faster.
2. Type II Response Curve: This is the most common type of functional response observed in nature, such as in rodents and weasels. At low prey density, the consumption rate increases at a decelerating rate. This is because predators spend more time searching for prey and the handling time per prey item is relatively low. As prey density increases, the rate of consumption continues to rise but at a slower rate due to limitations in handling time. Eventually, the rate of consumption reaches a plateau as handling time becomes the limiting factor.
3. Type III Response Curve: This type of response curve is also common in nature and shows a logistic increase in the rate of consumption with increasing prey density. At low prey density, the rate of consumption is relatively low due to factors such as difficulty in locating prey. As prey density increases, the rate of consumption rises rapidly, reaching a peak before leveling off or even declining as the predator’s ability to effectively exploit the abundant prey becomes saturated.

Numerical Response: The numerical response focuses on the population-level response of predators to changes in prey density. It describes how changes in prey density influence the population density of predators. Two main factors contribute to the numerical response:

1. Increased Fecundity: When prey density increases, predators have more access to food resources, which can lead to improved reproductive success. This results in increased birth rates and population growth rates among predators.
2. Aggregation Response: Prey aggregation in certain areas, also known as prey hotspots, can attract predators and increase their population density. When prey density is high in specific locations, predators tend to aggregate in these areas to maximize their foraging efficiency.

The combination of increased fecundity and aggregation response leads to an increase in predator population density with increasing prey density.

Understanding functional and numerical responses is crucial for comprehending the dynamics of predator-prey interactions and the stability of ecological systems. These responses provide insights into the mechanisms by which predators regulate prey populations and the feedback loops that exist between predator and prey populations.