Quantitative Inheritance in Plant Breeding

What is Quantitative Inheritance?

• Quantitative inheritance, often referred to as polygenic or multiple factor inheritance, is a crucial concept in genetics that addresses the heritability of traits influenced by multiple genes. Unlike qualitative traits, which exhibit clear phenotypic distinctions and are typically governed by single genes, quantitative traits manifest as measurable characteristics with a continuous range of variation.
• Quantitative traits encompass a broad spectrum of economically significant phenotypic attributes such as height, weight, skin pigmentation, and productivity measures in agriculture, such as crop yield or milk production. These traits do not show abrupt differences among individuals; rather, they exhibit continuous variation, where intermediate forms blend seamlessly from one phenotype to another. The concept of continuous variation was first introduced by Joseph Kolreuter in 1760 when studying the height of tobacco plants (Nicotiana).
• The underlying genetic architecture of quantitative traits involves multiple genes, termed polygenes, that each contribute a small, additive effect to the overall phenotype. These non-allelic genes work in concert, resulting in a cumulative influence on the trait. The collective effect of these genes can be challenging to discern through traditional Mendelian methods due to their subtle contributions, necessitating the use of statistical approaches for analysis.
• Historically, British mathematician Yule (1906) proposed that quantitative characters are controlled by numerous genes, a notion further developed by Mather, who introduced the term “polygenes.” Each polygene exerts a similar effect on the trait, and the total phenotype is influenced by the number of effective alleles present, aligning with the multiple factor hypothesis.
• One prominent example of quantitative inheritance is observed in the kernel color of wheat, where variations arise from the cumulative effects of several genes. Another example can be seen in maize (Zea mays), where ear size (cob length) illustrates the interplay of multiple genetic factors.

Characteristics of Quantitative Inheritance

Quantitative inheritance is a complex genetic phenomenon characterized by the inheritance of traits influenced by multiple genes. This type of inheritance plays a critical role in the expression of various traits in organisms, especially those that demonstrate continuous variation rather than discrete categories.

• Segregation at Multiple Gene Loci: The segregation of traits in quantitative inheritance occurs across an extensive number of gene loci. This means that rather than being determined by a single gene, quantitative traits arise from the cumulative effects of many genes, each contributing to the overall phenotype.
• Trivial Effects of Allelic Substitutions: In quantitative traits, substitutions of alleles at specific gene loci often have negligible effects on the phenotype. This characteristic underscores the complexity of gene interactions, where the addition or alteration of a single allele does not significantly change the observable traits.
• Interchangeable Phenotypic Effects: Genes associated with multiple traits may perform different biochemical functions but yield similar phenotypic outcomes. Therefore, the effects of gene substitutions can often be interchangeable, allowing for a range of phenotypic expressions while maintaining overall functionality.
• Genetic Blocks and Inversions: Genes may be organized into blocks that are connected by inversions, which are then transmitted as cohesive units from inversion heterozygotes to their offspring. However, crossing over can disrupt these blocks in insertion homozygotes, demonstrating the intricate dynamics of genetic recombination in quantitative inheritance.
• Pleiotropic Effects of Polygenes: Polygenes, which are responsible for quantitative traits, exhibit pleiotropic effects, meaning that a single gene can influence multiple phenotypic traits. Although an allele may function in a specific biochemical pathway, its effects can extend beyond a single characteristic, impacting various traits simultaneously.
• Environmental Influences on Phenotypic Expression: Environmental conditions play a significant role in shaping the phenotypic expression of polygenes responsible for quantitative traits. For instance, the height of plants such as corn, tomatoes, peas, and marigolds is a genetically controlled quantitative trait. However, environmental factors—including soil quality, fertility, moisture levels, temperature, light exposure, and even the presence of parasites—can substantially affect growth and development. Moreover, identical twins, despite sharing the same genotype, can display different intelligence quotients when raised in distinct environmental conditions, further illustrating the interplay between genetics and environment.

Examples of Quantitative Inheritance

1. Kernel Colour in Wheat

The inheritance of kernel color in wheat represents a fascinating study in quantitative genetics, primarily conducted by the Swedish geneticist Herman Nilsson Ehle in 1908. His work focused on hybridizations between red kernel-colored and white kernel-colored wheat varieties, revealing significant insights into the genetic control of this trait.

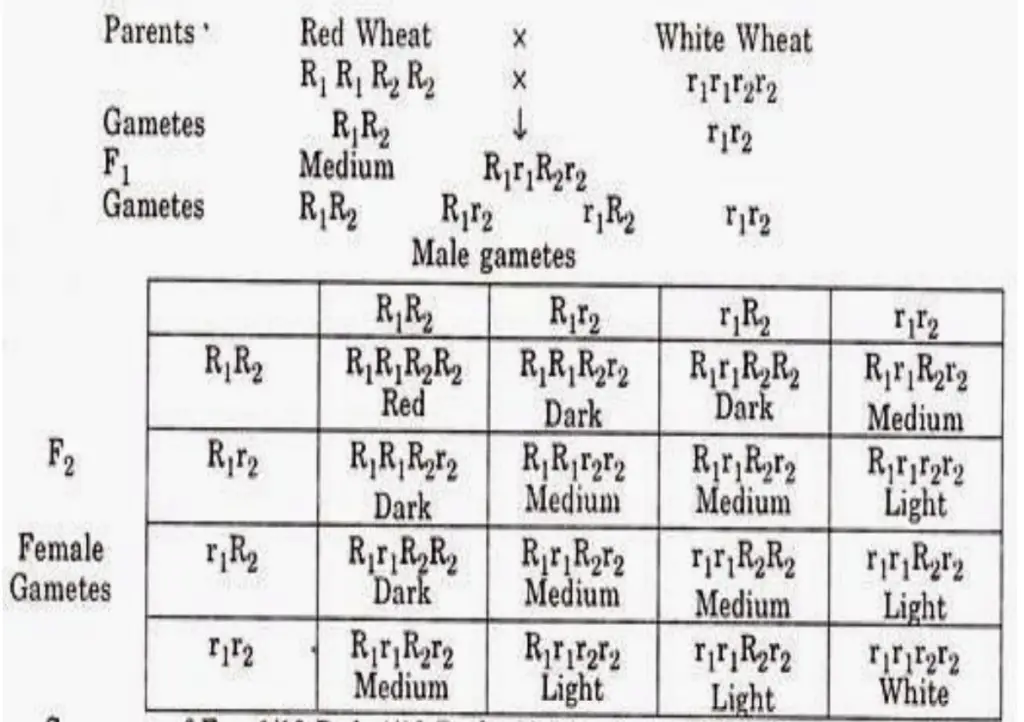
• Hybridization Experiments: Ehle performed various crosses between red and white kernel varieties. In the F1 generation, the heterozygous hybrids exhibited a lighter red kernel color, indicating an intermediate phenotype compared to the homozygous red parents.
• F2 Phenotypic Ratios: The F2 generation revealed varying phenotypic ratios in different hybridizations, such as 3 red to 1 white, 15 red to 1 white, and 63 red to 1 white. These ratios, alongside the continuous variation observed from red to white kernels, suggested a complex inheritance pattern.
• Genetic Basis: Nilsson Ehle proposed that the kernel color in wheat is regulated by three genes, each possessing two alleles. One allele contributes to red grain color (the effective allele), while the other allele results in white grain color (the non-contributing allele). Therefore, the presence of these contributing alleles plays a pivotal role in determining the kernel color.
• Cumulative Effect of Alleles: Each contributing allele for red kernel color contributes a small degree of red pigment. The overall phenotypic expression of kernel color results from the additive effects of all contributing alleles. Consequently, each additional dose of a pigment-contributing allele enhances the intensity of red color in the wheat kernels.
• Example Cross: To illustrate this, consider a cross between a red kernel-colored wheat variety with the genotype AABB (which has four contributing alleles) and a white kernel-colored variety with the genotype aabb (which has no contributing alleles). The F1 hybrids, resulting from this cross, possess the genotype AaBb, leading to a medium red color due to the presence of two contributing alleles.
• Gamete Formation and F2 Generation: The F1 hybrids can produce four types of gametes: AB, Ab, aB, and ab. The random fusion of these gametes during fertilization leads to 16 potential combinations in the F2 generation. Out of these combinations, 15 yield red kernel color, while one results in white kernels. This leads to the observed ratio of 15 red to 1 white in the F2 generation.
• Continuous Variation in F2 Progeny: The F2 progeny exhibit continuous variation in kernel color, primarily influenced by the number of effective alleles present. Among the F2 population, the distribution of phenotypes includes:
  • 1/64 with the genotype AABBCC, showcasing deep red kernels.
  • 6/64 with five contributing alleles, demonstrating dark red kernels.
  • 15/64 possessing four contributing alleles, presenting red kernels.
  • 20/64 with three contributing alleles, resulting in medium red kernels.
  • 15/64 with two contributing alleles, reflecting light red kernels.
  • 6/64 with one contributing allele, exhibiting very light red kernels.
  • 1/64 with the genotype aabbcc, leading to white kernels.
• Phenotypic Classes: The resulting phenotypic classes reveal a ratio of 1 deep red: 6 dark red: 15 red: 20 medium red: 15 light red: 6 very light red: 1 white, illustrating the continuous nature of variation in kernel color.
• Environmental Influences: Kernel color in wheat is also considered a quantitative trait influenced by environmental factors. Variables such as temperature, sunlight, and nutritional availability can alter enzyme activity and substrate levels, resulting in phenotypic variations within each genotype. This highlights the dynamic interaction between genetic and environmental components in the expression of quantitative traits.

2. Ear size (Cob length) in Maize(Corn, Zea mays)

The ear, or cob, of maize (corn) serves as the structure that houses the kernels, all of which are protected by layers of leaves known as husks. The inheritance of ear size, specifically cob length, has been a significant area of study in genetics, notably examined by American geneticists Emerson and East in 1913. Their research provides a detailed understanding of the genetic mechanisms underlying this trait.

• Hybridization Studies: Emerson and East began their investigation by crossing a long-eared variety known as Black Mexican Sweet corn, which averages 16.8 cm in ear length and ranges from 13 cm to 21 cm, with a short-eared variety called Tom Thumb Popcorn, which has an average ear length of 6.6 cm, ranging from 5 cm to 8 cm. This hybridization was designed to elucidate the genetic basis for variations in ear size.
• F1 Generation Observations: The resulting F1 progeny displayed ears of intermediate length, measuring between 9 cm and 15 cm, with an average length of 12.1 cm. This observation indicated that the trait for cob length was not simply dominant or recessive but rather exhibited intermediate inheritance.
• F2 Progeny and Variation: Upon examination of the F2 generation, a continuous variation in cob length was observed, showcasing a wide range of lengths. Some plants produced ears that closely resembled those of the short-eared grandparent, while others had longer ears similar to those of the long-eared parent. However, the majority of the F2 progeny exhibited ear lengths akin to that of the F1 hybrids.
• Genetic Control: Emerson and East concluded that the size of the ear in maize is determined by two genes, each with two alleles, thereby demonstrating a polygenic (quantitative) inheritance pattern. The absence of effective alleles results in a baseline ear length equivalent to that of the Tom Thumb Popcorn parent, averaging 6.6 cm.
• Cumulative Effect of Alleles: The length of the cob is directly influenced by the number of contributing alleles present in the genotype. Each contributing allele adds a small, consistent increment to the overall cob length. Specifically, it was determined that each contributing allele increases the ear length by 2.55 cm, calculated as follows: (16.8 cm – 6.6 cm) divided by 4 (the total number of effective alleles).
• Phenotypic Class Distribution in F2 Progeny: In the F2 generation, the distribution of ear sizes based on contributing alleles is as follows:
  • 1/16 of the progeny possess 4 contributing alleles (genotype AABB), yielding an average ear size of 16.8 cm, similar to the Black Mexican Sweet corn.
  • 4/16 have 3 contributing alleles (genotypes AABb, AaBB), resulting in an average ear length of 14.2 cm.
  • 6/16 possess 2 contributing alleles (genotypes AaBb, AAbb, aaBB), which averages to 11.7 cm.
  • 4/16 have 1 contributing allele (genotypes Aabb, aaBb), producing an average ear size of 9.1 cm.
  • 1/16 exhibit no contributing alleles (genotype aabb), corresponding to the average ear size of 6.6 cm, like the Tom Thumb Popcorn parent.
• Phenotypic Class Ratio: The phenotypic distribution among the F2 progeny results in five classes of ear sizes with a ratio of 1: 4: 6: 4: 1, illustrating the continuous variation in ear length across the population.
• Environmental Influences: As a quantitative trait, ear size in maize is also subject to environmental influences. Factors such as temperature, sunlight exposure, and nutritional availability can significantly impact the growth and development of the cobs, leading to variability even among plants with the same genetic makeup.

3. Skin Colour in Man

Skin color in humans is a classic example of polygenic inheritance, a genetic mechanism where multiple genes contribute to a single trait. This complexity is particularly evident in the study of skin pigmentation differences among populations, such as between individuals of African descent and those of European descent. Research conducted by Davenport in 1913 in Jamaica elucidates the genetic factors influencing this trait.

• Genetic Basis: According to Davenport, skin pigmentation is primarily influenced by two pairs of alleles, designated as A-a and B-b. These alleles contribute to the skin color phenotype in an additive manner, meaning that the presence of dominant alleles leads to darker pigmentation while recessive alleles result in lighter skin.
• Parental Genotypes: In this model, a true Negro individual is represented by the genotype AABB, possessing four dominant genes, whereas a Caucasian individual exhibits the genotype aabb, which contains four recessive genes. This clear distinction forms the foundation for exploring the inheritance of skin color.
• F1 Generation: When these two parent types are crossed, the resulting F1 offspring all carry the genotype AaBb. These individuals exhibit an intermediate skin color, commonly referred to as mulatto, which reflects the combined genetic contributions of both parents.
• F2 Generation and Phenotypic Variation: The mating of two mulatto individuals (AaBb x AaBb) leads to the F2 generation, which demonstrates a remarkable range of skin colors among the offspring. The phenotypic variation observed in this generation can be categorized into five distinct groups:
  • Black (Negro): Represented by the genotype AABB.
  • Dark: Associated with genotypes AaBB or AABb.
  • Intermediate: Corresponding to the genotype AaBb.
  • Light: Linked to genotypes aaBB or Aabb.
  • White: Reflecting the genotype Aabb or aa bb.
• Genotypic Frequency and Ratios: The results from the F2 generation yield specific frequencies of the genotypes leading to various phenotypes. This results in a phenotypic ratio of approximately:
  • 1 Black (AABB)
  • 4 Dark (AaBB, AABb)
  • 6 Intermediate (AaBb)
  • 4 Light (Aabb)
  • 1 White (aa bb)
• Additive Effects of Genes: The findings suggest that the A and B genes exert approximately equal influence on the degree of skin pigmentation. Consequently, variations in the number of these alleles present in an individual will result in corresponding changes in skin color, demonstrating how genetic combinations can lead to a spectrum of phenotypic expressions.

4. Height in Man

Height in humans serves as a prime example of polygenic inheritance, showcasing the intricate interplay between genetics and environmental factors in determining phenotypic traits. Unlike simpler traits governed by a limited number of genes, human height is influenced by the combined effects of numerous genes, leading to a wide range of adult heights.

• Complex Genetic Control: The inheritance of height involves approximately ten or more pairs of genes. Each of these genes contributes to an individual’s overall height, with the effect of each gene being additive. Therefore, the more dominant alleles an individual possesses, the greater the influence on their height phenotype.
• Recessive and Dominant Alleles: In the context of height, the character of tallness is recessive, meaning that an individual must inherit a sufficient number of recessive alleles to express this trait. Conversely, individuals with a higher proportion of dominant alleles will exhibit a shorter phenotype. This genetic basis illustrates how an individual’s genotype can result in significant variations in their height.
• Range of Height: Adult human heights exhibit substantial variability, typically ranging from 140 cm to 203 cm. This broad spectrum underscores the multifactorial nature of height, influenced not only by genetic composition but also by external factors.
• Environmental Influences: Height is not solely determined by genetics; it is also affected by various environmental conditions. Factors such as nutrition, health during developmental years, and socio-economic status can all contribute to an individual’s final height. For instance, a diet rich in essential nutrients during childhood and adolescence can promote optimal growth, while malnutrition may stunt it.
• Normal Distribution Curve: When analyzing the heights of a large population, such as measuring a thousand adult men, one can observe that the distribution of heights typically forms a bell-shaped curve, known as the normal distribution. This curve represents the statistical variation in height across the population and is a hallmark of quantitative traits. The central peak indicates the average height, while the tails of the curve reflect the extremes of shorter and taller individuals.
• Quantitative Trait Characterization: Height exemplifies a quantitative trait because it is influenced by multiple genes and exhibits continuous variation. The normal distribution of height measurements signifies that while most individuals cluster around the average, there are still considerable proportions of individuals who fall at both extremes of the height spectrum.

Salient Features of Quantitative/Polygenic Inheritance

Quantitative or polygenic inheritance refers to the genetic mechanism whereby multiple genes, known as polygenes, collectively influence a particular phenotypic trait. This form of inheritance is characterized by a range of features that illustrate the complexity of trait expression in organisms.

• Governance by Multiple Genes: Quantitative traits are regulated by multiple genes or polygenes, rather than a single gene. This means that many different genetic loci contribute to the overall phenotype, leading to a more nuanced expression of traits.
• Continuous Variation in Phenotype: The expression of these polygenes results in continuous variation in the phenotypes of individuals. Unlike traits governed by single genes, which often exhibit discrete categories, quantitative traits can take on a wide spectrum of values, such as height or skin color.
• Environmental Influence: The environment plays a significant role in the expression of polygenic traits. Factors such as nutrition, climate, and overall health can impact the phenotypic expression, demonstrating the interplay between genetic predisposition and environmental conditions.
• Statistical Analysis of Polygenes: Polygenic traits can be subjected to statistical analysis to assess the number of genes contributing to a particular trait. Techniques such as quantitative trait locus (QTL) mapping can be utilized to identify the genetic loci responsible for the variations observed in these traits.
• Additive Effects of Genes: Each gene within a polygenic trait contributes a unit effect or individual effect. Consequently, the overall impact of the genes is additive or cumulative, meaning that the effects of different alleles sum up to produce the final phenotype. This additive nature emphasizes the complexity of polygenic traits.
• Partial or Absent Dominance: In polygenic inheritance, dominance is either absent or partial. For example, the F1 hybrid often exhibits blending of the parental traits, resulting in an intermediate phenotype. This blending is a hallmark of polygenic inheritance, as it contrasts with the clear-cut dominance seen in single-gene traits.
• Segregation at Multiple Loci: Unlike Mendelian traits, where segregation occurs at a single locus of homologous chromosomes, polygenes segregate at multiple loci. This multi-locus segregation contributes to the continuous range of phenotypic expression observed in the offspring.
• Independent Assortment: Polygenes assort independently in the F2 generation, adhering to Mendelian principles. However, the resulting phenotypes are not limited to discrete classes but instead fall within a continuous range that spans between the extreme limits of the parental phenotypes.
• Modified Phenotypic Proportions: The phenotypic proportions of the F2 progeny are modified based on the number and nature of the genes involved. The interaction among multiple alleles can lead to varying ratios of phenotypes, reflecting the underlying genetic architecture.
• Pleiotropic Effects: Polygenes often exhibit pleiotropic effects, meaning they can influence multiple traits simultaneously. This complexity adds another layer to the understanding of how certain genes can have widespread impacts on the organism’s overall phenotype.

Population Genetics: Hardy-Weinberg’s Law

Population genetics examines the distribution and change in allele frequencies within populations, often in the context of evolutionary theory. One fundamental concept in this field is Hardy-Weinberg’s Law, which serves as a model for understanding genetic structure in populations. This law provides a framework for predicting how allele and genotype frequencies will remain constant over generations under specific conditions.

• Definition of a Population: A population consists of a group of individuals belonging to the same species, occupying a defined geographic area, and capable of interbreeding. These individuals interact and exchange genetic materials, thus influencing the genetic makeup of future generations.
• Historical Context: In 1908, mathematician G. H. Hardy and physician W. Weinberg independently formulated a quantitative theory to describe the genetic structure of populations. Their work laid the groundwork for the Hardy-Weinberg principle, which quantifies expected genotype frequencies in a population based on certain assumptions.
• Statement of Hardy-Weinberg Law: The Hardy-Weinberg Law asserts that “the relative frequencies of genes in a large, panmictic population after random mating remain constant from generation to generation in the absence of evolutionary processes such as migration, mutation, selection, and genetic drift.” This means that allele and genotype frequencies in a population will remain stable if certain criteria are met.
• Conditions for Hardy-Weinberg Equilibrium: The Hardy-Weinberg principle describes a theoretical scenario in which a population experiences no evolutionary changes. For the law to hold true, several conditions must be met:
  • Absence of Evolutionary Forces: There must be no mutation, selection, genetic drift, or migration impacting the population. These forces can alter allele frequencies and disrupt genetic equilibrium.
  • Large Population Size: The population must be sufficiently large to minimize the effects of random sampling errors that can lead to genetic drift.
  • Random Mating: Individuals within the population must mate randomly, ensuring that gametes combine without bias toward any specific genotype.
  • Equal Gamete Production: Each parent must produce approximately equal numbers of gametes, ensuring that no genetic advantages are conferred to any group within the population.
• Implications of Hardy-Weinberg Law: Under these ideal conditions, the gametes produced by individuals combine randomly, resulting in constant gene frequencies across generations. The genetic equilibrium for the genes in question is thus maintained, preserving the variability present within the population. Specifically, the law predicts that both allele frequencies and genotype frequencies will remain stable in an infinitely large interbreeding population.
• Mathematical Representation: The Hardy-Weinberg Law can be expressed mathematically, typically through the equation p2+2pq+q2=1p^2 + 2pq + q^2 = 1p2+2pq+q2=1, where:
  • ppp represents the frequency of the dominant allele,
  • qqq represents the frequency of the recessive allele,
  • p2p^2p2 indicates the frequency of homozygous dominant individuals,
  • 2pq2pq2pq represents the frequency of heterozygous individuals,
  • q2q^2q2 denotes the frequency of homozygous recessive individuals.
• Significance in Evolutionary Biology: The Hardy-Weinberg principle serves as a null hypothesis in population genetics, allowing researchers to identify whether observed allele frequencies in a population deviate from the expected frequencies due to evolutionary forces. This framework aids in the understanding of population dynamics and evolutionary processes.

Conditions of the Hardy-Weinberg Population

The Hardy-Weinberg Principle serves as a cornerstone of population genetics, providing a mathematical framework to understand how allele and genotype frequencies remain stable in a population over time, given specific conditions. This principle emphasizes that certain conditions must be met to maintain genetic equilibrium within a population. Below are the key conditions necessary for a population to adhere to the Hardy-Weinberg equilibrium.

• Large Population Size: The population must be large enough to prevent random fluctuations in allele frequencies. In small populations, chance events can lead to significant deviations in genetic structure over generations, a phenomenon known as genetic drift. Therefore, a large population mitigates the effects of these random sampling errors.
• Random Mating: Mating among individuals in the population must occur randomly, meaning there should be no preferential selection for certain genotypes over others. If certain traits confer a reproductive advantage, the frequency of alleles associated with those traits could increase, leading to changes in the genotype frequencies over generations. Thus, random mating is crucial for maintaining the expected allele frequencies.
• No Migration: The population must be isolated in terms of gene flow. This means that there should be no emigration (individuals leaving the population) or immigration (individuals entering the population) that could introduce or remove alleles from the gene pool. Migration can alter allele frequencies and disrupt the equilibrium.
• Absence of Mutations: There should be no new mutations that could introduce new alleles or change existing ones. Mutations are a source of genetic variation, and their occurrence would violate the assumption of constant allele frequencies within the population. Therefore, for Hardy-Weinberg equilibrium, the mutation rate must be negligible.
• No Incestuous Mating: Incestuous or inbreeding mating, where closely related individuals breed, should be avoided. Inbreeding can lead to an increased expression of deleterious recessive traits, which may affect overall fitness and reproductive success. Hence, maintaining genetic diversity is essential for a stable population.
• Implications of Hardy-Weinberg Principle: The Hardy-Weinberg Principle predicts that if all the aforementioned conditions are satisfied, the distributions of genotype frequencies will remain constant across generations. The frequencies of alleles will be in equilibrium, as expressed in the equation:p2+2pq+q2=1 Here, ppp represents the frequency of one allele, while qqq represents the frequency of the alternate allele at a specific locus. The terms p2, 2pq, and q2 correspond to the frequencies of the homozygous dominant, heterozygous, and homozygous recessive genotypes, respectively.
• Understanding Genetics: To grasp the significance of the Hardy-Weinberg equilibrium, it is essential to understand basic genetics principles. Initially, the concept of inheritance was thought to function through a blending mechanism, where offspring would display intermediate traits of their parents. However, this theory was challenged by Darwin’s natural selection, which requires variation among traits to enhance survival and reproduction.
• Mendelian Genetics: The principles of inheritance were further elucidated by Gregor Mendel’s experiments with pea plants, which demonstrated that traits are determined by discrete units called alleles. Each individual possesses two alleles for every gene (being diploid), but only one allele from each parent is passed on to the offspring through gametes. This random selection ensures that allele frequencies remain consistent unless affected by external evolutionary pressures.
• Genotype Combinations: For any given locus, if two alleles exist, an individual could possess the following genotype combinations: homozygous dominant (e.g., CC), homozygous recessive (e.g., cc), or heterozygous (e.g., Cc). If a heterozygote’s phenotype resembles that of one of the homozygotes, the allele linked to the observed trait is classified as dominant, while the other is recessive. This hierarchical relationship between alleles underpins much of classical genetics.

The Hardy-Weinberg Principle Explained

The Hardy-Weinberg principle serves as a foundational concept in population genetics, providing a mathematical framework to analyze allele and genotype frequencies in sexually reproducing diploid organisms. This principle predicts that, under certain conditions, allele frequencies within a population will remain stable across generations.

• Constant Allele Frequencies: One of the core predictions of the Hardy-Weinberg principle is that the allele frequencies in a population will not change from generation to generation, provided that specific conditions are met. This concept is essential for understanding genetic stability within populations, particularly in the absence of external evolutionary pressures.
• Genotype Frequencies: The Hardy-Weinberg principle further specifies that for a population with two alleles at a locus, denoted as ppp and qqq, the expected genotype frequencies can be derived using the formula:p², 2pq, q² In this formula, p² represents the frequency of homozygous dominant individuals (e.g., genotype CC), 2pq corresponds to the frequency of heterozygous individuals (e.g., genotype Cc), and q² indicates the frequency of homozygous recessive individuals (e.g., genotype cc).
• Relationship Between Alleles: Given that there are only two alleles at a locus, the principle stipulates that the sum of their frequencies must equal one:p+q=1 This relationship is fundamental to understanding how allele frequencies contribute to the overall genetic makeup of a population.
• Equilibrium Conditions: The Hardy-Weinberg principle assumes that a population is in a state of Hardy-Weinberg equilibrium, which occurs only under specific conditions. These conditions include a large population size, random mating, no migration, the absence of mutations, and no selection pressures. When these conditions are satisfied, the genotype frequencies will remain constant across generations, reflecting the stability of the population’s genetic structure.
• Implications for Evolutionary Biology: The significance of the Hardy-Weinberg principle extends beyond mere mathematical relationships; it provides a baseline against which researchers can compare actual population data. Deviations from the expected genotype frequencies can indicate the presence of evolutionary forces such as natural selection, genetic drift, or gene flow.
• Application in Research: By applying the Hardy-Weinberg principle, biologists can assess whether a population is evolving or remaining stable. For instance, if a population shows a significant shift in allele frequencies over generations, it suggests that one or more of the equilibrium conditions have been violated, prompting further investigation into the factors influencing those changes.