Use Spearman’s rank correlation and Pearson’s linear correlation to analyse the relationships between two variables, including how biotic and abiotic factors affect the distribution and abundance of species (the formulae for these correlations will be provided, as shown in the Mathematical requirements)

SouravNovember 1, 2024

Answer

To analyze the relationships between two variables, particularly how biotic and abiotic factors affect the distribution and abundance of species, we can utilize two statistical methods: Spearman’s rank correlation and Pearson’s linear correlation. Each method has its own application based on the nature of the data being analyzed.

1. Pearson’s Linear Correlation

Description: Pearson’s correlation coefficient (denoted as $r$) measures the strength and direction of the linear relationship between two continuous variables. It assumes that both variables are normally distributed and that there is a linear relationship between them.

Formula:

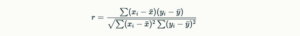
Description: Spearman’s rank correlation coefficient (denoted as $\rho$ or rsrs​) assesses how well the relationship between two variables can be described using a monotonic function. It is non-parametric and does not assume normal distribution, making it suitable for ordinal data or non-linear relationships.

Formula:

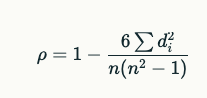
Where:

• di​ is the difference between the ranks of each pair of values,
• n is the number of pairs.

Application:

• Data Collection: Rank the data for two variables, such as soil moisture content (abiotic factor) and insect diversity (biotic factor).
• Analysis: Calculate $\rho$ using the formula to evaluate the strength of the monotonic relationship.
• Interpretation:
  • Values close to +1 indicate a strong positive monotonic correlation.
  • Values close to -1 indicate a strong negative monotonic correlation.
  • A value around 0 suggests no monotonic correlation.